线性表
GitHub地址
求star(`・ω・´)
总述
代码是抽象的——所以我们学习数据结构时尽量自己把图给画出来,自己去模拟这个过程,才能加深印象。
线性链表的创建
这里我们采用while循环创建链表,当输入某一个特定的值(-9999)时停止创建。
基本思路
- 首先创建三个node指针,一个指向头
head,一个指向尾p,一个作为开辟新结点的工具q。 (代码第4行) - 记得将
head初始化为空,然后让p = head(注意,此时的head和p都没有“实体”结点,都指向NULL)。 (代码第4, 5行) head为空:正常地new然后赋值,接着让p指向head; (代码第9~14行)head不为空:new一个新结点q,对两个成员变量进行赋值。让p->link指向q,接着让p指向新的“尾巴”p = q。 (代码第16~22行)- 返回
head即可。 (代码第26行)
出现过的问题
- 创建的表的首结点会重复两次。原因就在于☆处,没有再次输入n,导致n的值被用于创建首结点和第二个结点。
需要注意的点
- 特殊情况:空表和只有一个结点。
代码
NODE* create_link()
{
int n;
NODE* head = NULL, * p, * q;
p = head;
cin >> n;
while (n != -9999)
{
if (head == NULL) {
head = new NODE;
head->data = n;
head->link = NULL;
p = head; //p只需要指向head即可
☆ cin >> n; //还是需要一个cin,不然n的值没法更新,第一个就会创建两次
}
else{
q = new NODE; //用q创建,然后p再指
q->data = n;
q->link = NULL;
p->link = q;
p = q;
cin >> n;
}
p->link = NULL;
}
return(head);
}
线性链表的插入
基本思路
- 首先确定位置的三种情况:0,中间,>链表长度。其中,后两种可以合成一种情况讨论。
- 对于插在头结点的情况,我们直接添加(详情查看代码)。
- 对于另外的情况,首先要让指针指到要插入的位置。然后进行插入。
需要注意的点
- 分类讨论,插在表头的特殊情况
- 传递的参数需要是引用。 有没有直接传递指针就可以改变的方法呢?
- (接上一行)有!返回类型设置为
NODE*,然后head = insert_link(head)就行了
代码
// NODE* insert_link(NODE *head)
void insert_link(NODE *head) {
int loc; //作用:记录要插入的位置
cout << "Where do you want to insert?\n";
cin >> loc;
loc -= 1; //在原来结点的前面插入
NODE* pos = head; //作用是指向要插入的位置
//insert
int num; //该结点的值
cout << "please input the number\n";
cin >> num;
NODE* q = new NODE; //开始创建新的结点
q->data = num;
if (loc == -1) { //problem: 返回后一切不变,传递的不是指针吗?
q->link = head;
head = q; //为什么它不会改变?传递的是指针,必须要引用指针?
}
else {
//find the position
while (pos->link != NULL && loc) { //为什么它不会触发等于NULL的条件?因为↓
pos = pos->link; //不可以直接用pos++
loc--;
}
q->link = pos->link;
pos->link = q;
}
//return head; 如果传回指针,就加这句。
}
线性链表的删除
删除链表中值为a的 第一个/所有 结点。
基本思路
- 确定特殊情况:为空链表、删除的是头结点
- 对于一般情况,即删除的结点在中间。让2个指针指向被删除结点及其前面的结点,然后将前面的结点的link接到下下个结点上,再
delete要删除的结点即可。 - 对于为空,直接返回传入的参数
head即可。 - 对于头结点,先
用q保存本结点的地址,然后直接让head指向下一个结点,再删除原头结点即可。
需要注意的点
- 讨论好特殊情况即可
代码
void delete_link(NODE* head, int a) { //此处只需要传入头结点即可
if (head == NULL) { //链表为空时
cout << "链表为空!\n";
return ;
}
NODE* q = head;
if (q->data == a) { //删除的是头结点
head = q->link; //由于前面已经保存head结点,所以直接接上去,再删除
delete(q);
return ;
}
else { //删除的是中间结点
NODE* p = head; //作用:指向要删除的结点的前面
while (q->data != a && q->link != NULL) { //为了找到匹配的结点
p = q;
q = q->link;
}
if (q->data == a) { //是因为找到了才停下来的
p->link = q->link; //接上去
delete(q); //删除该结点
return ;
}
else { //是因为到尾了才停下来的
cout << "未找到对应的结点!\n";
return ;
}
}
}
线性链表的反转
这个操作应该算是最难的操作之一了,我也是画了很久的图才理清关系的。
我画了个图,方便理解。
基本思路
- 首先确定特殊情况:空表或者只有一个结点,有多个情况
- 对于空表或者只有一个结点的情况,只需要返回传进来的
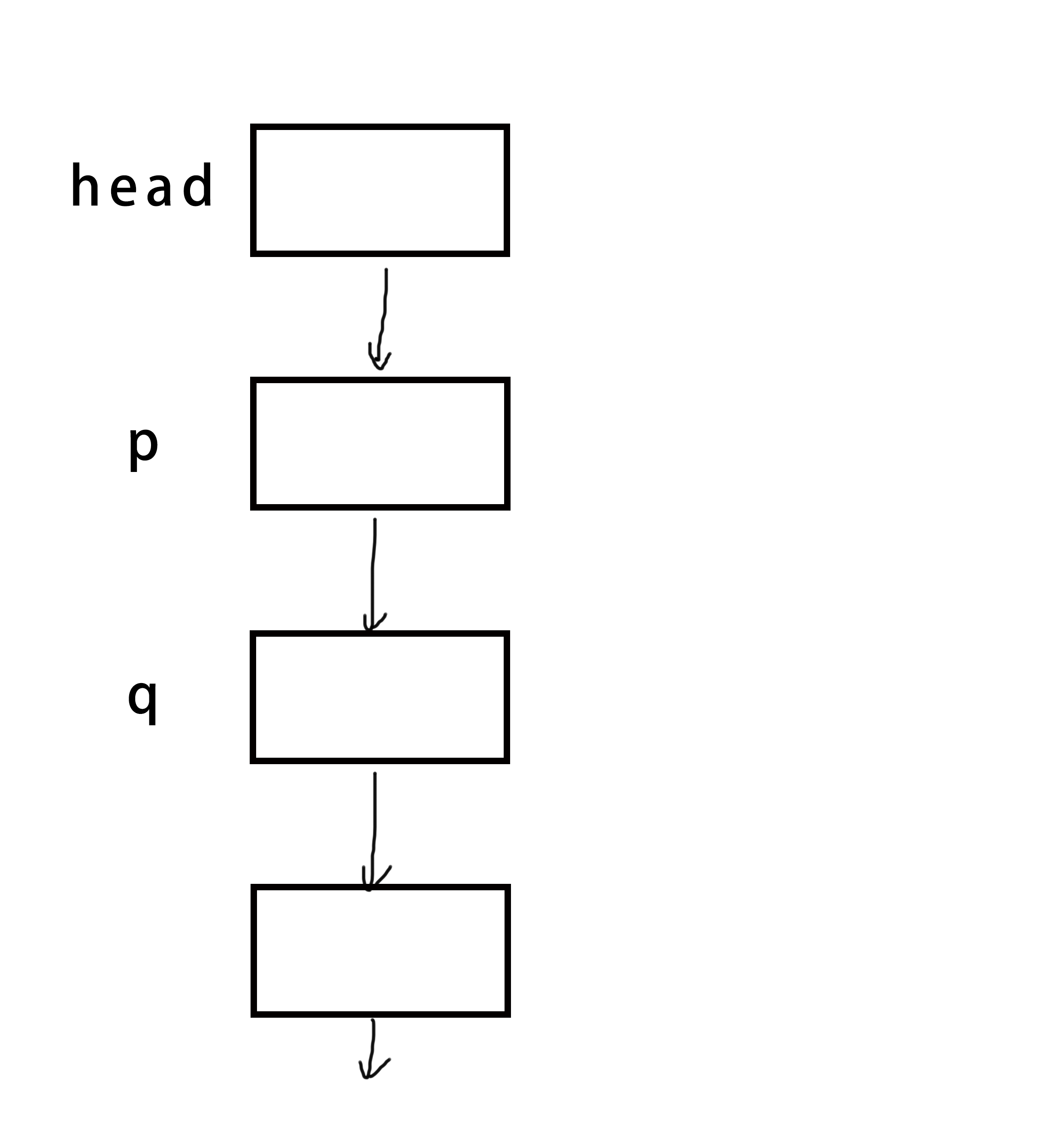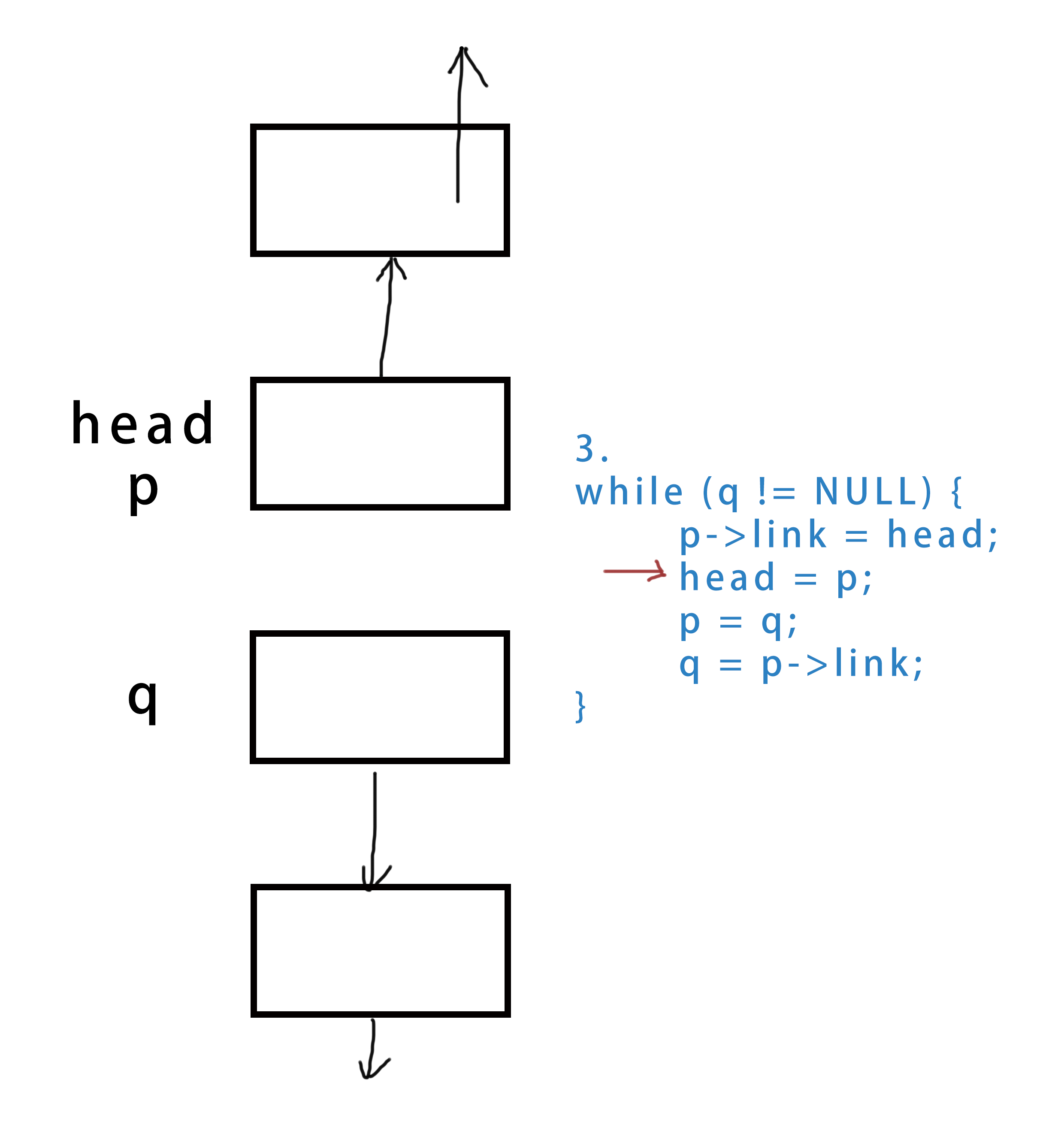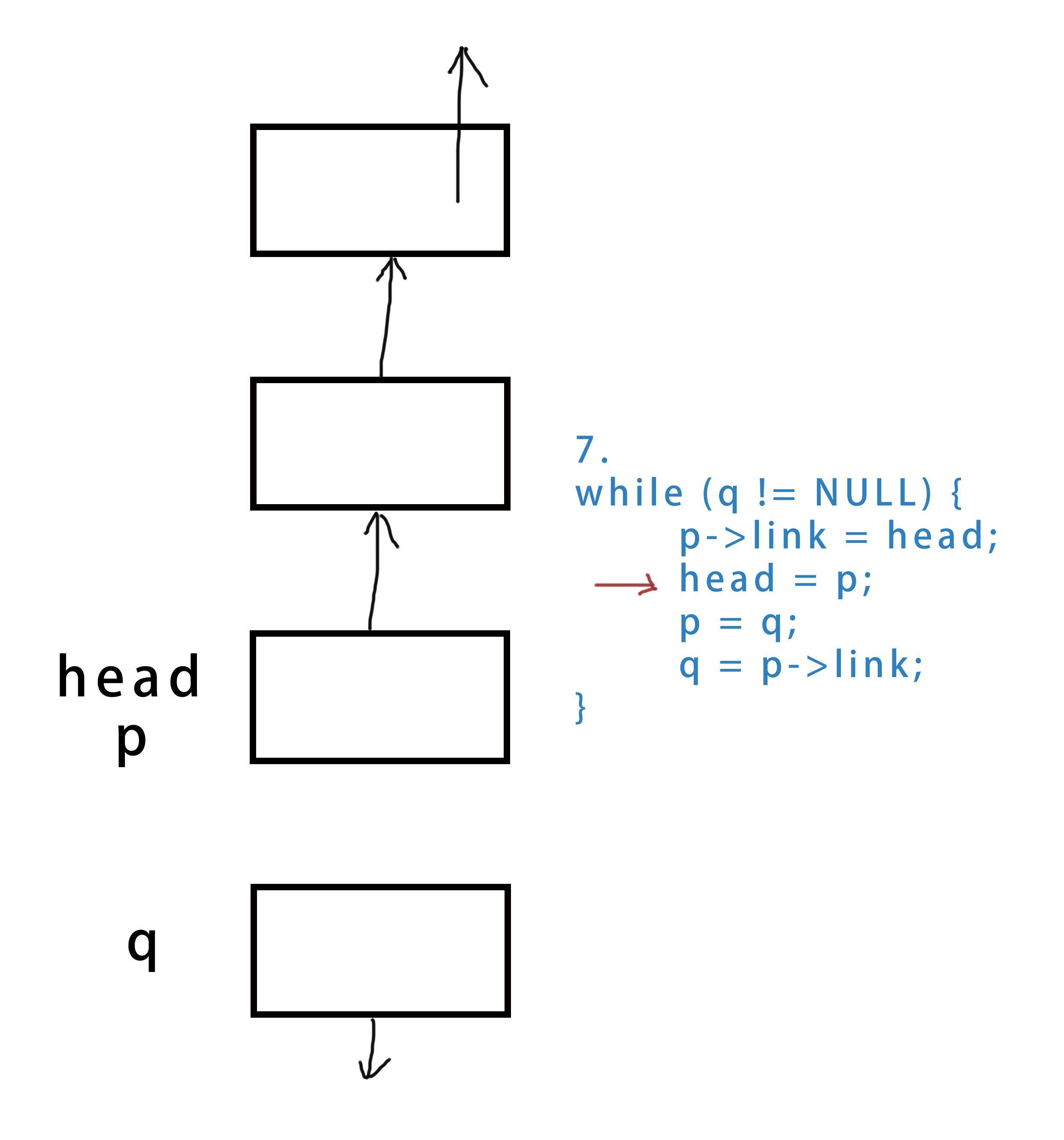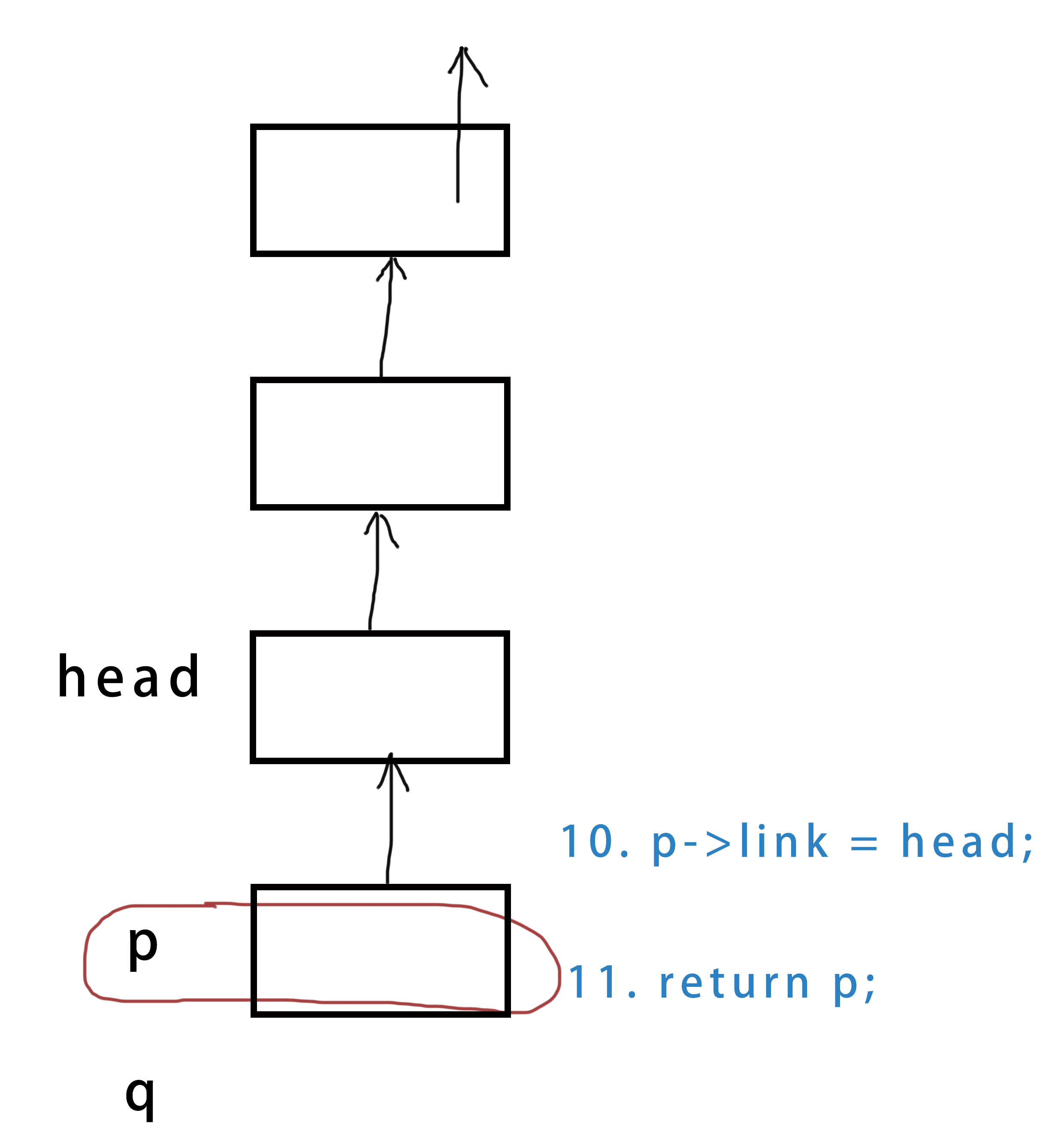
head即可。 - 对于多个结点的反转情况,我们使用三个指针保存三个相邻的结点(下文称为“上、中、下”)。将中间结点接到上结点,然后整体下移一个结点,直到下结点为空为止。
需要注意的点
- !!!逻辑千万要理清!!!
代码
NODE* reverse_link(NODE* head) {
if (head == NULL || head->link == NULL) return head; //空表或者只有一个结点相当于不需要反转
NODE* p = head->link;
NODE* q = p->link;
head->link = NULL;
while (q != NULL) {
p->link = head; //将“中间”结点指向上一个结点
head = p; //以下三句相当于把这三个指针整体向后移动一个
p = q;
q = p->link; //p->link还是q->link都一样,用p->link为了方便理解
}
p->link = head; //最后一个结点还没有连到倒数第二个上面
return p;
}
线性链表多项式相加
基本思路
- 基本思路包含在代码注释中了(累了,实在是不知道该怎么写了…)
需要注意的点
- 需要注意的是,与前面的不同,这里使用了全新的NODE结点。
代码
#include <iostream>
#include<ctime>
#include <Windows.h>
using namespace std;
const int n1 = 8; //n为多项式1最高次
const int n2 = 8; //n为多项式2最高次
struct NODE {
int coef; //项的系数
int exp; //项的次数
NODE* link;
};
//插入结点(仅可传入指向尾巴的指针)
NODE* insert(NODE* pc, int c, int e)
{
NODE* t;
t = new(NODE);
t->coef = c;
t->exp = e;
pc->link = t;
return(t);
}
//为了方便调试,创建随机的多项式,次数从高到低
NODE* create_randLink(NODE* link, int n) {
NODE *tail = link;
if (n == 0) return NULL;
if (link == NULL) { //没有就创建头结点
link = new NODE;
link->coef = rand() % 20 - 10;
link->exp = n;
link->link = NULL;
tail = link;
n--;
}
else { //如果有头结点就找到尾巴
while (tail->link != NULL)
tail = tail->link;
}
srand((unsigned)time(NULL));
while(n--) { //n为项的次数,从高次到低次插入结点
NODE* t;
t = new NODE;
t->coef = rand() % 20 - 10; //系数范围:-10~9 (可能并不是)
t->exp = n;
t->link = NULL;
tail->link = t; //尾巴接上新结点
tail = t;
}
return link;
}
//输出多项式
void outputPoly(NODE* head) {
bool isFirst = true;
while(head->link != NULL;) { //停止于尾结点
if (head->coef == 0) continue;
else if (head->coef > 0) {
if (isFirst) { //如果是多项式的第一项
cout << head->coef << "x^" << head->exp;
isFirst = false;
}
else {
cout << " + " << head->coef << "x^" << head->exp;
}
}
else {
if (isFirst) { //如果是多项式的第一项
cout << "-"<< -head->coef << "x^" << head->exp; //由于负号和数字在一起不便于观察,便和正项统一格式
isFirst = false;
}
else {
cout << " - " << -head->coef << "x^" << head->exp;
}
}
head = head->link;
}
if (head->coef > 0) { //此时已经是尾结点了,由于每个次数的结点都存在,所以这个一定是常数
cout << " + " << head->coef;
}
else if (head->coef < 0) {
cout << " - " << -head->coef;
}
cout << "\n\n";
}
//将两个多项式相加,返回相加结果的头指针
NODE* polyadd_1(NODE* ah, NODE* bh)
{
NODE* pa, * pb, * ch, * pc;
char c;
ch = new(NODE);
pc = ch;
pa = ah;
pb = bh;
while (pa != NULL && pb != NULL)
{
if (pa->exp == pb->exp) c = '='; //没想到居然是因为老师的''中间有空格,所以无限循环
else if (pa->exp > pb->exp) c = '>';
else c = '<';
switch (c)
{
case '=': //如果次数相等,直接插入相加后的结果
if (pa->coef + pb->coef != 0)
pc = insert(pc, pa->coef + pb->coef, pa->exp);
pa = pa->link;
pb = pb->link;
break;
case '>': //次数不等,先统一次数
pc = insert(pc, pa->coef, pa->exp);
pa = pa->link;
break;
case '<': //次数不等,先统一次数
pc = insert(pc, pb->coef, pb->exp);
pb = pb->link;
break;
}
}
while (pa != NULL) //如果b到头,但a没有
{
pc = insert(pc, pa->coef, pa->exp);
pa = pa->link;
}
while (pb != NULL) //如果a到头,但b没有
{
pc = insert(pc, pb->coef, pb->exp);
pb = pb->link;
}
pc->link = NULL;
pc = ch;
ch = ch->link;
delete pc;
return(ch);
}
int main() {
NODE* linkOne = NULL, *linkTwo = NULL, *linkTh = NULL;
linkOne = create_randLink(linkOne, n1);
outputLink(linkOne);
Sleep(1000); //防止运行过快,导致两个多项式一样
linkTwo = create_randLink(linkTwo, n2);
outputLink(linkTwo);
linkTh = polyadd_1(linkOne, linkTwo);
outputLink(linkTh);
return 0;
}
环形链表
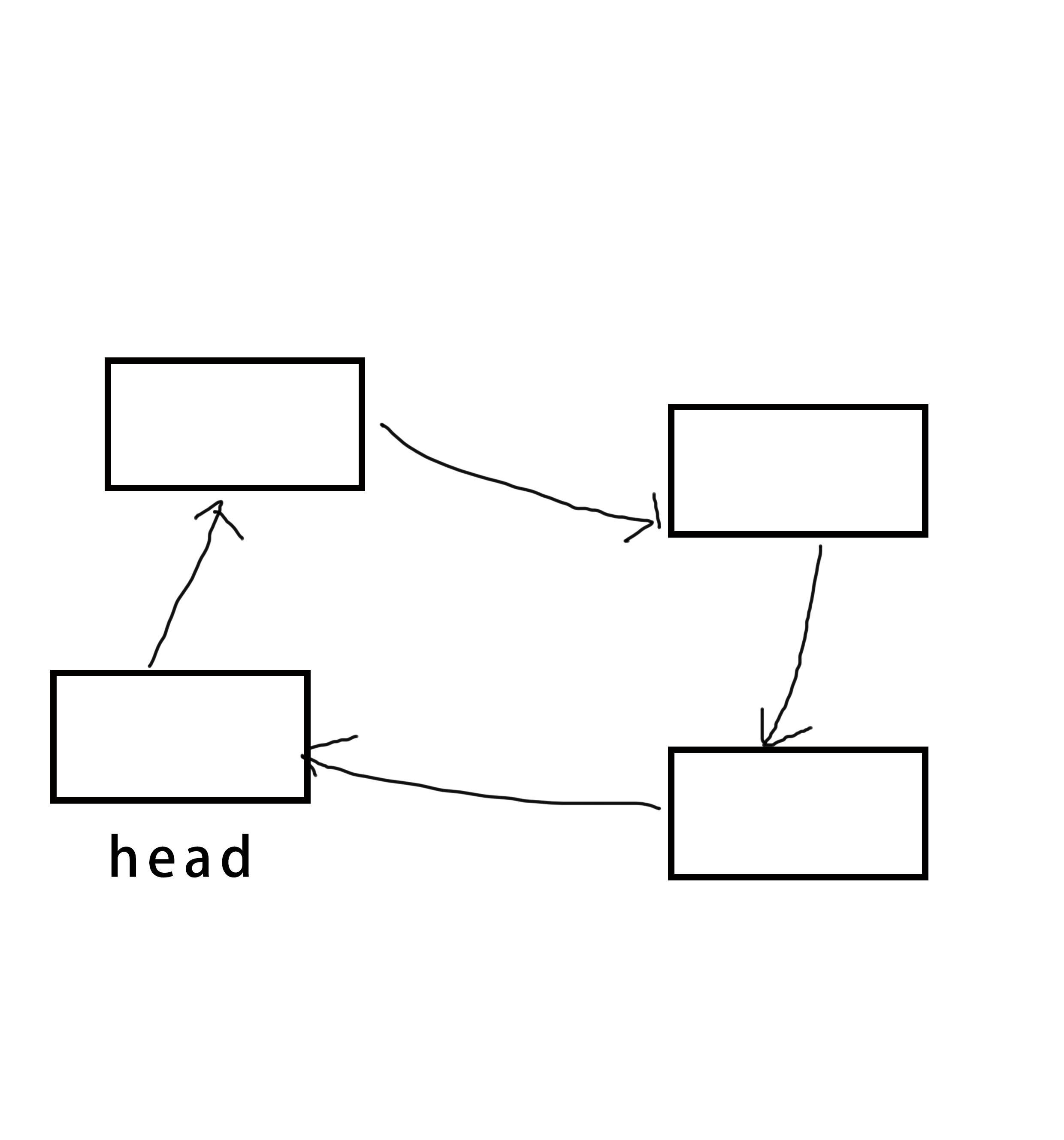
基本思路
- 与非环形单向链表差不多,只是尾结点指向头结点而不是空。
需要注意的点
- 首先是输出的判定问题,可以先创建一个指针从头结点的下一个位置开始,当达到头结点时停止输出。
- 然后就是创建、插入、删除、反转等操作中需要更改的地方。需要在建立新结点(以
q为例)后,将q->link = NULL改成q->link = head,其他照常不变。 - 很重要的一点就是,是否有头结点。如果有头结点,则头结点不储存数据或者把储存的数据作为结束标志;如果没有,直接将头指针指向第一个结点即可。
代码
以创建为例
//带头结点的单向循环多项式链表的创建
node* createPoly(node *head, int num)
{
if (head == NULL) { //如果头结点不存在,就创建头结点
head = new node;
head->coef = 0;
head->exp = -1; //作为结束标记点,便于输出的识别
head->link = head;
}
node* p = head, * q; //p指向最后一个结点,q指向新的结点
int n;
cout << "请输入次数为:"<< num << "的系数(输入-9999提前停止):";
cin >> n;
while (n != -9999) {
q = new node;
q->coef = n;
q->exp = num;
q->link = head; //创建新结点q并对其赋值
p->link = q;
p = q; //将新结点接上
num--; //它的位置至关重要
if (num < 0) break;
cout << "请输入次数为:" << num << "的系数(输入-9999提前停止):";
cin >> n;
}
return head;
}
//不带头点的单向循环多项式链表的创建
node* create_link()
{
int n;
node* head = NULL, * p, * q; //q:创建新结点,p:指向尾结点
p = head;
cin >> n;
while (n != -9999)
{
if (head == NULL) { //如果首结点不存在便创建
head = new node;
head->data = n;
head->link = head;
p = head; //尾结点接上去
cin >> n;
}
else {
q = new node; //q是创建新结点
q->data = n;
q->link = head;
p->link = q; //尾结点接上去
p = q;
cin >> n;
}
p->link = head;
}
return(head);
}
双向链表
此处我们主要讨论非循环的双向
基本思路
- 对于循环的双向链表,创建时可以直接在
head前面添加结点。 - 非循环双向与循环双向的区别在于头尾结点是否相连,所以道理是通的。
- 第一个结点的左右结点为自己,后面的结点都可以用类似于“递归”的思想创建下去。
需要注意的点
- 由于比单向的多了一个成员变量,所以复制过来需要仔细修改。
代码
//双向带头结点的非循环链表
struct node {
int data;
node* llink, * rlink;
};
node* createLink() {
node* head = NULL ;
//head->data = -9999; head->llink = NULL; head->rlink = head; //头结点不是链表中的内容
node* p, * q;
int n;
cout << "请输入数据(-9999结束):";
cin >> n;
if (n == -9999) {
return head;
}
else {
head = new node;
head->data = n;
head->llink = NULL; //循环结点的话,此处为自己
head->rlink = NULL; //同上
p = head;
cout << "请输入数据(-9999结束):";
cin >> n;
}
while (n != -9999) {
q = new node;
q->data = n; q->llink = p; q->rlink = NULL; //建
p->rlink = q;
p = q; //尾结点更新
cout << "请输入数据(-9999结束):";
cin >> n;
}
return head;
}
总结
- 创建链表的思路基本都是分为两个部分:头结点和非头结点部分。
- 对于其他各种操作来说,讨论好头尾中三部分的操作就行,剩下的就是怎么接。
- 加新结点的思路一般都是创建新结点->连接到原来的结点上去。容易错的地方就是输入
data的位置。
