字符串匹配算法
BF(Brute Force)算法
算法思路
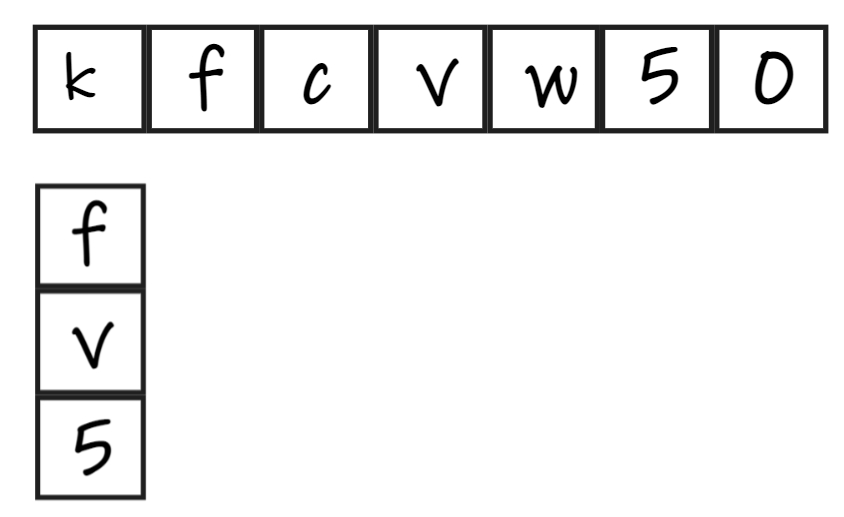
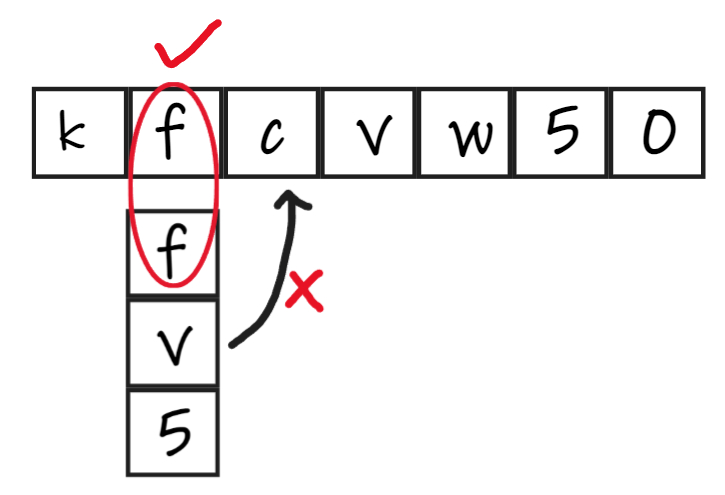
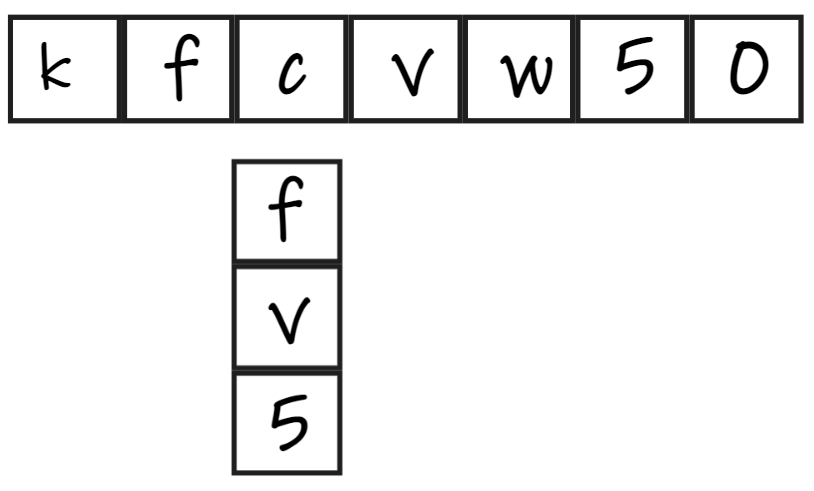
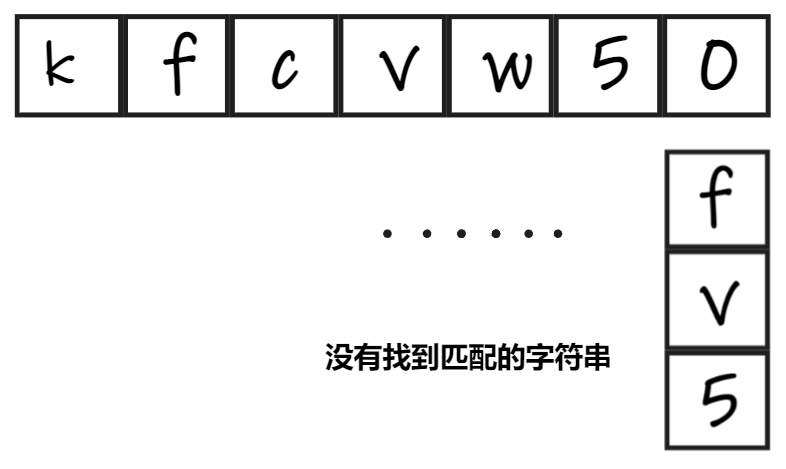
BF算法是暴力算法,主要思路为:
将模式串的首字符与主串逐一比对,如果匹配,则比对各自的接下来一位;如果不匹配,后移,继续重复前面所说的比对。
时间复杂度分析
设模式串的长度为m,主串长度为n,那么时间复杂度为O(n*m)
代码
int bruteForce(string main, string sub) {
int len_m = main.length();
int len_s = sub.length(); //首先获取两个字符串的长度
if (len_m < len_s) return -1; //模式串比主串大,直接返回
for (int i = 0; i < len_m; i++) { //遍历main字符串的每一个字符
if (main[i] == sub[0]) { //比较首字母,如果匹配就比较后面的
int tem = i + 1; //复制这个位置,
int j = 1; //j: 遍历sub的剩下字符
for (; j < len_s && tem < len_m; j++, tem++) { //任意一方到头就退出
if (main[tem] != sub[j]) //如果有不匹配的,直接退出
break;
}
if (j == len_s) return i; //如果是j退出,返回该位置。注意此时的j是因为到了len_s才退出的
}
}
return -1; //找不到匹配的就返回-1
}
KMP(Knuth-Morris-Pratt)算法
简要介绍
KMP算法是由三个人联合发表的字符串匹配算法,是BF算法的改进版。
KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。
具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。
KMP算法的时间复杂度O(m+n)。
算法思路
-
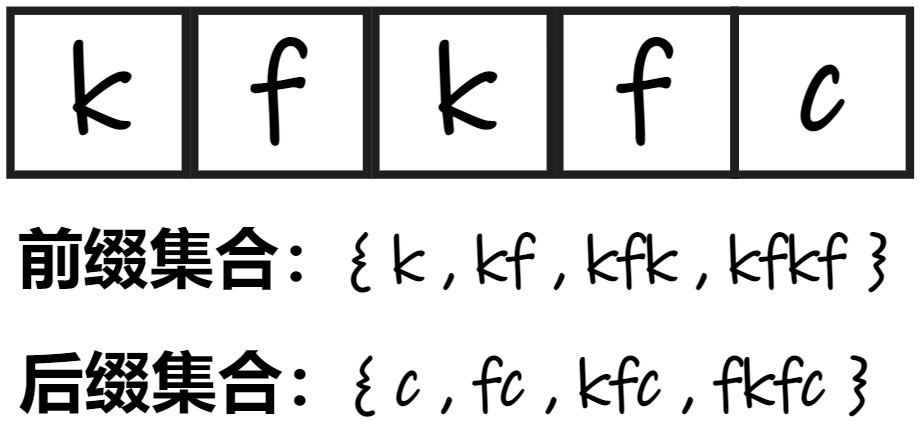
首先理解前后缀
- 前缀:从该字符串开头的不间断的真子串。
- 后缀:从该字符串末尾往前的不间断的真子串。
-
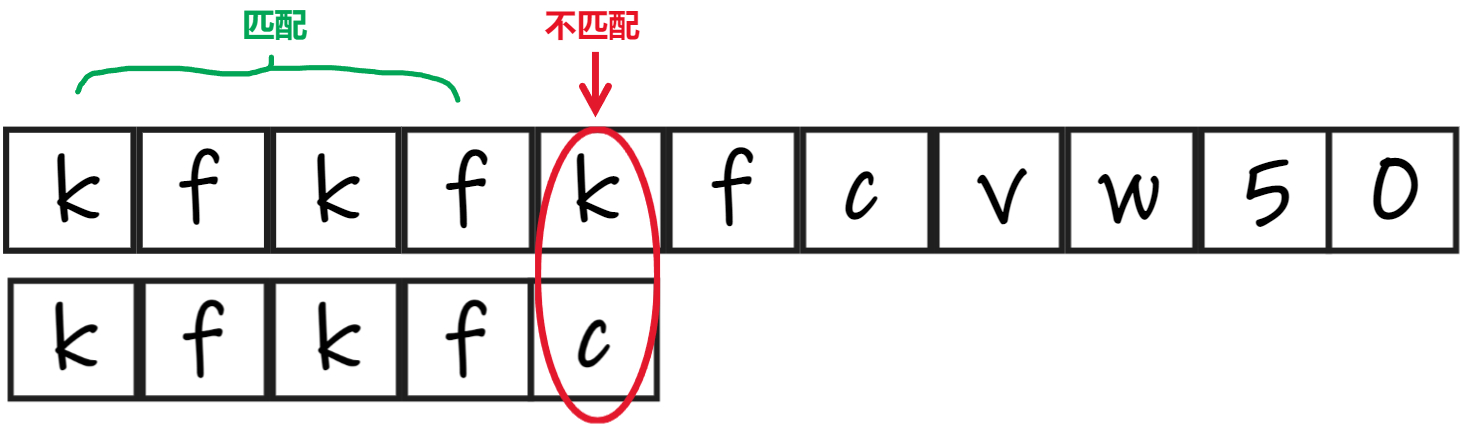
我们的目的是:减少匹配次数。
- 当两串中某个字符不匹配时,它所包含的信息不仅仅是“该字符不匹配”,还有“前面的字符是匹配的”。
- 所以,如果充分利用这些信息,我们就可以减少匹配次数。
-
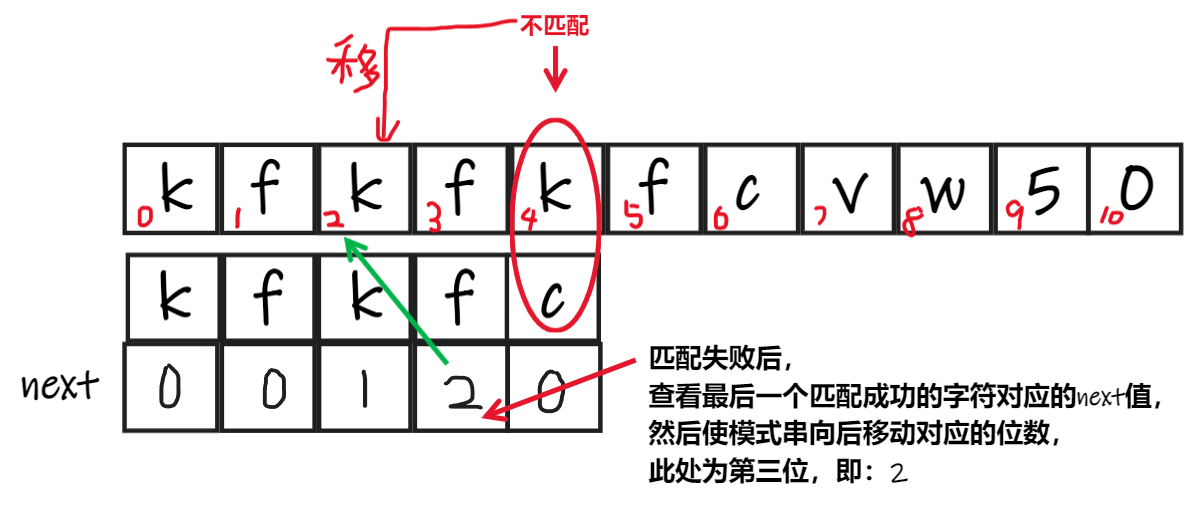
如何利用这些信息——next数组
- 当遇到不匹配内容时,KMP算法会查看最后一个匹配的字符所对应的next值,这个值就是模式串要后移到的位置(代码中体现为指向模式串字符的指针回溯的值)。
- 因为前、后缀必定包含首尾字符,所以某个字符对应的next值也表示匹配前缀的第几位。
- 这样,问题的重心就落到了next数组的构建上。
-
next数组的构建
- 由于我们是利用两串已匹配的部分的信息(因为遇到不匹配,还表示前面是匹配的),所以主串和模式串的这一部分是相同的。
- 而我们构建next数组需要找到“主串的后缀集合”与“模式串前缀集合”的交集中的最长的元素,所以这里可以看作是寻找“模式串的后缀集合”与“模式串前缀集合”,即模式串的自匹配。
- next数组第i位的数字表示模式串第 i 位前的子串中的最大相等前后缀的长度。
- 构建过程总共分为四步:
- 初始化
- 若前后缀不相同:回退到初始位置(0)或者相等的位置
- 若前后缀相同:指向后缀的指针后移一位
- next:把前缀的长度赋给该字符(指向前缀,永不往回走的指针指向的字符)对应的next值。
- 注意此处的“指向后缀”的值等于“前缀的长度。
补充说明——next数组的构建
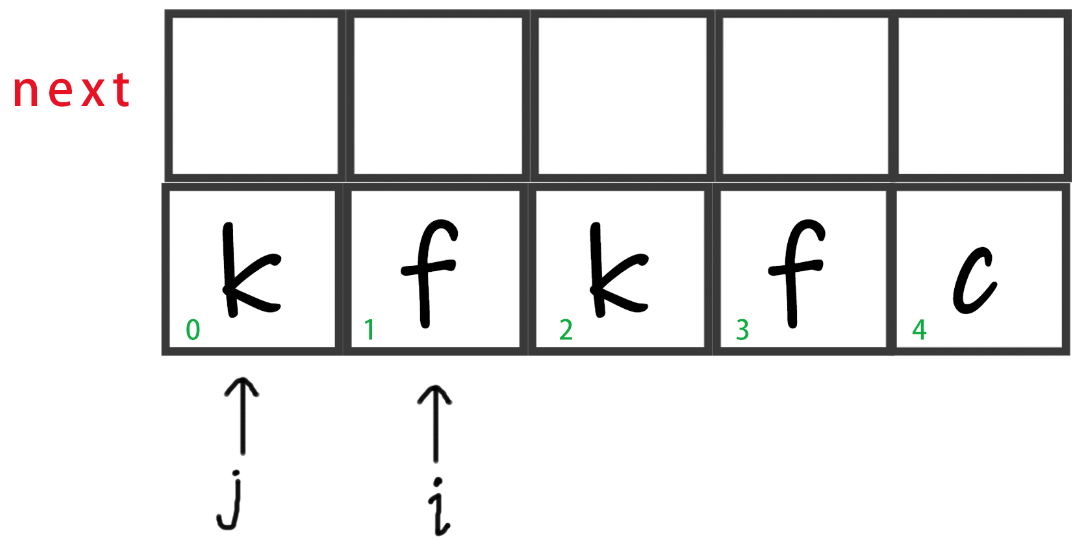
简要说明:
- 最上方是next数组
- 第二行是模式串,下文用变量
str指代。 - 第二行左下角的绿色数字代表模式串和next数组的下标。
- i、j的值等于其指向的格子的左下角的数字。
-
首先初始化,令
j = 0;。而由于str[0]没有匹配的前后缀(不可能是自己),所以我们令next[0] = j,即等价于next[0] = 0。
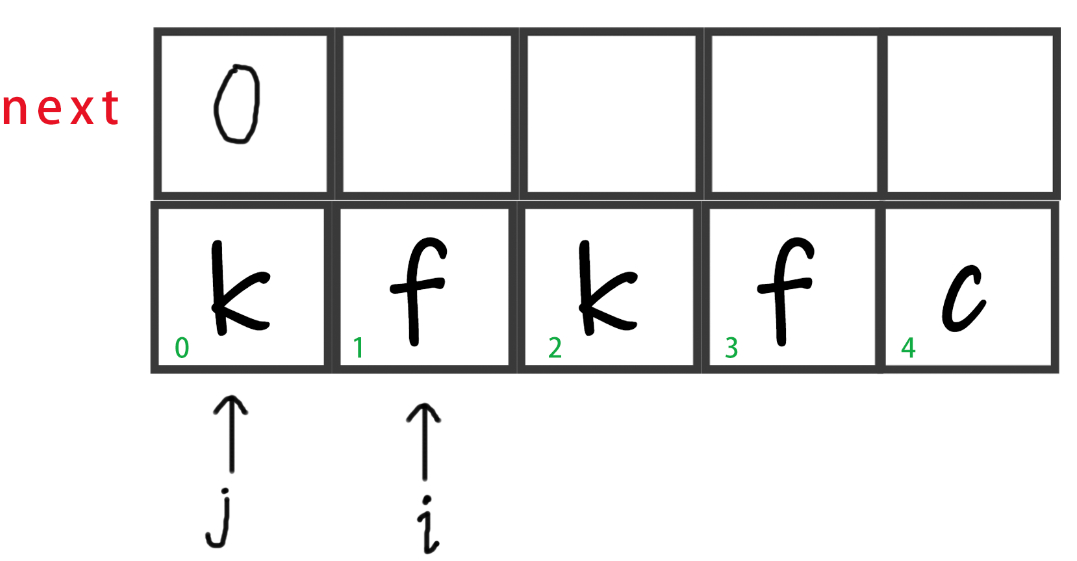
-
然后进入
for循环,for里面令i = 1,即从第二个字符开始。此处我们可以看到str[i] != str[j],而j又是在开头,所以我们直接走第四步,让next[i] = j,即等价于next[1] = 0。
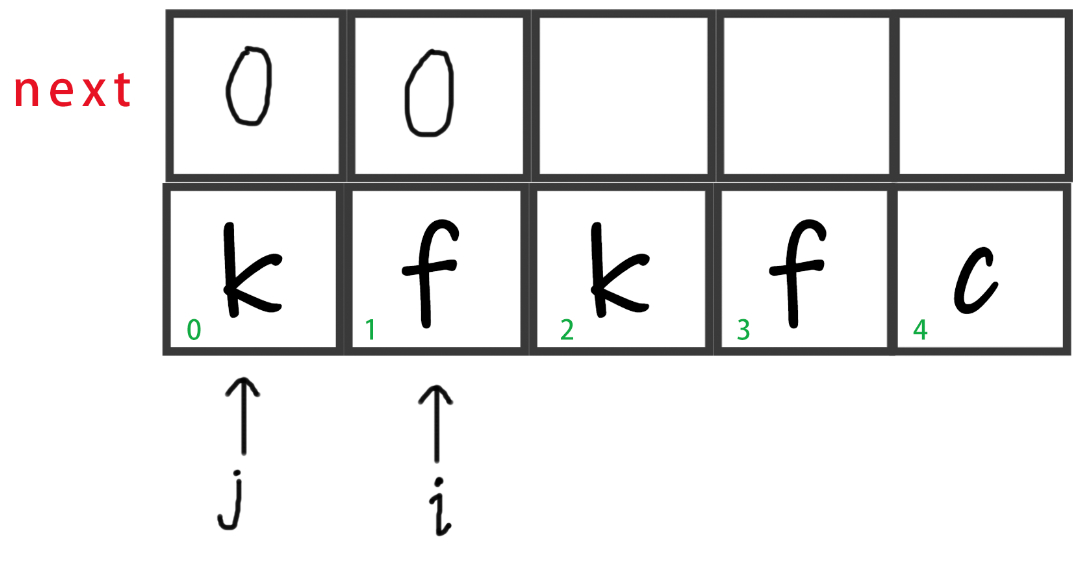
-
循环继续下去,此时i往后移一位,即
i++。注意我们求最大相等前后缀的串都是i及其前面的,i后面的不用管。
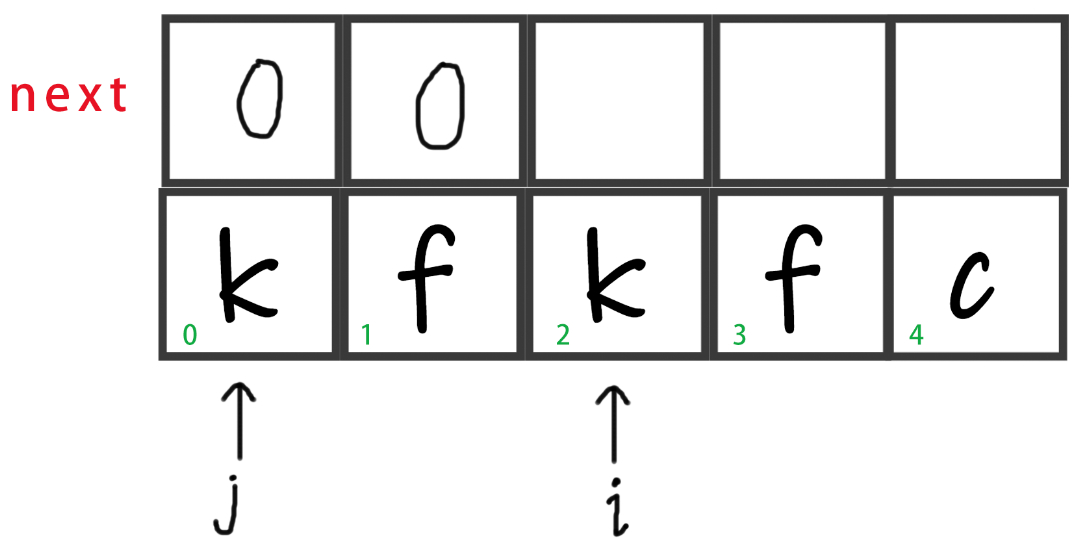
-
此时
str[i] == str[j],即str[2] == str[0] == 'k'。所以我们令j++。
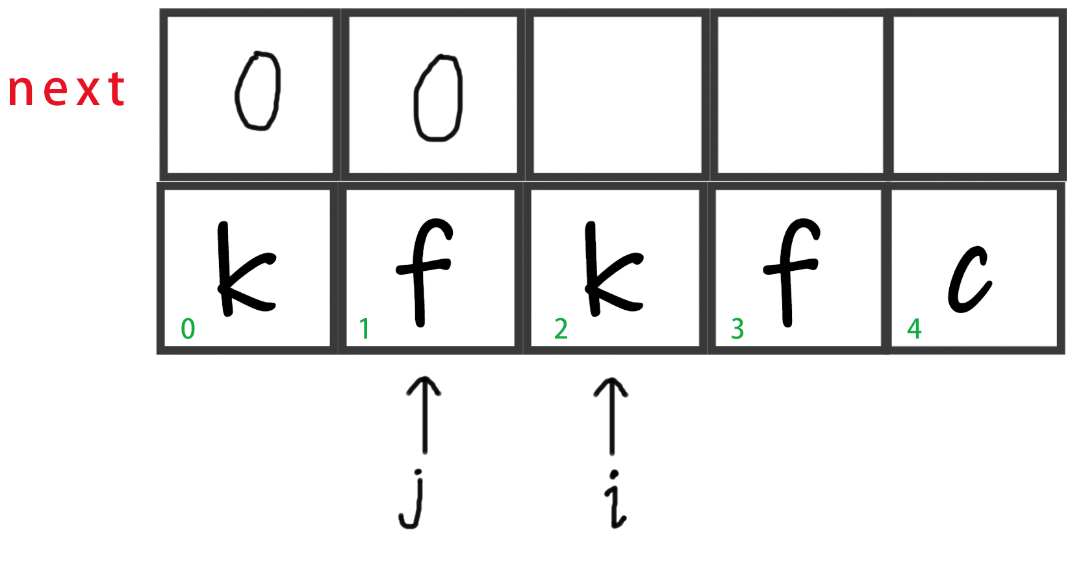
-
接下来就要给next赋值了,令
next[i] = j,即next[2] = 1。表示在str[0]到str[2]中,最大相等前后缀的长度为1。
而由于前缀必定是从首字符开始的,所以这个 1 也表示str[1]前的字符串(不包括str[1]) 与 从str[2]开始(包含str[2])往开头方向数的 1 个字符匹配。
-
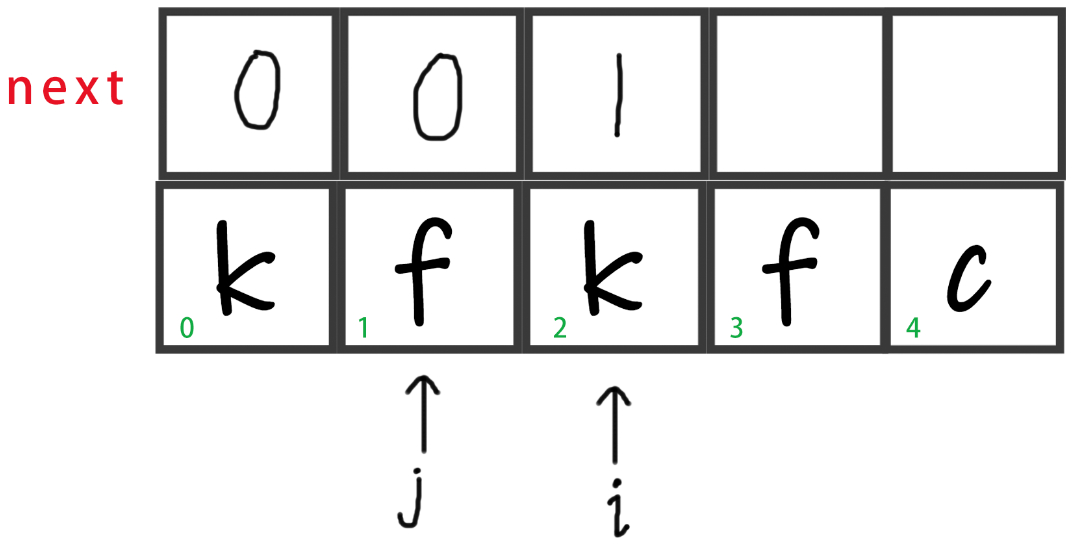
循环继续下去,此时i往后移一位,即
i++。
-
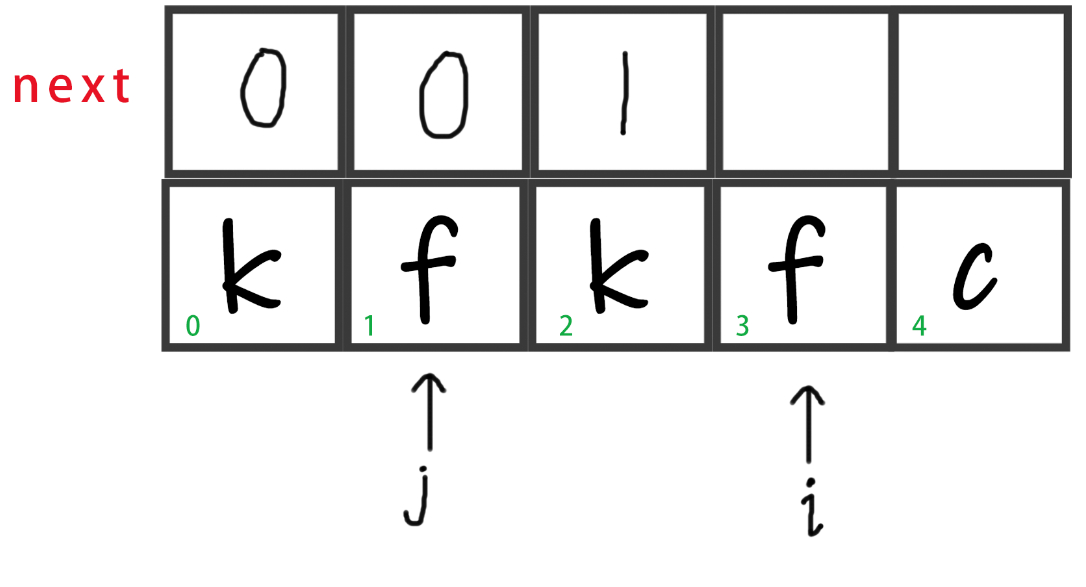
此时
str[i] == str[j],即str[3] == str[1] == 'f'。所以我们令j++。
-
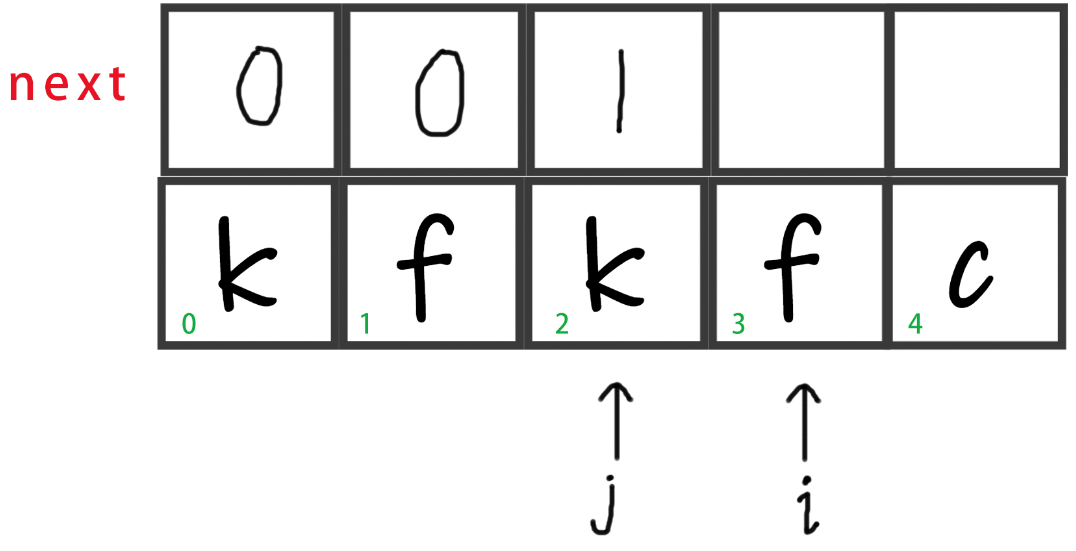
又到了给next赋值的时候了,令
next[i] = j,即next[3] = 2。表示在str[0]到str[3]中,最大相等前后缀的长度为2。
这个 2 表示str[2]之前的字符串(不包括str[2]) 与 从str[3]开始(包含str[3])往开头方向数的 2 个字符匹配。
这一点跟第 5 点很像,我把它抽象成:
这个 j 表示`str[j]`之前的字符串(不包括`str[j]`)
与
从`str[i]`开始(包含`str[i]`)往开头方向数的 j 个字符匹配。
其中,j == next[j]
-
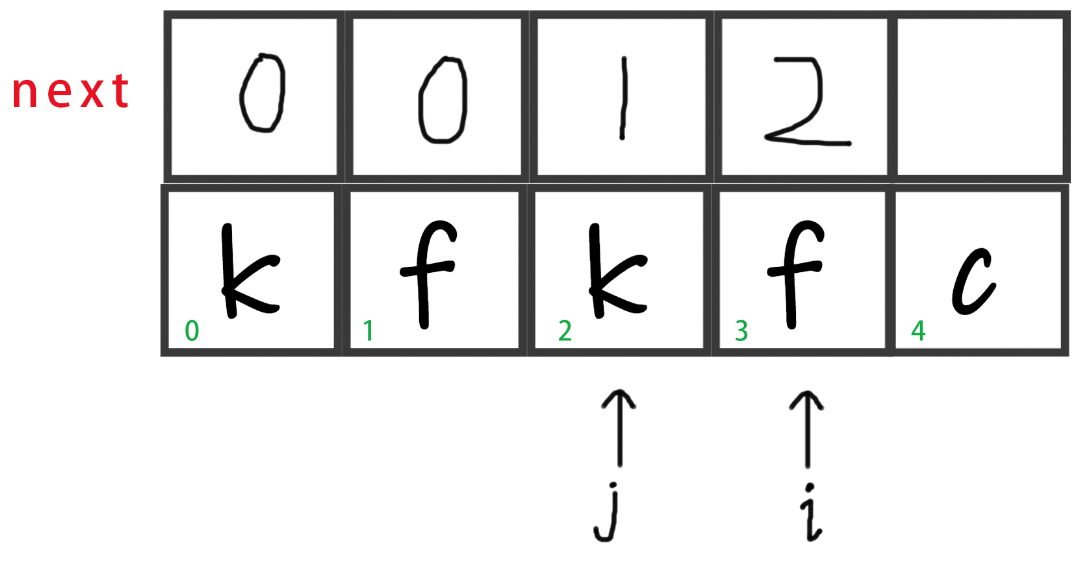
循环继续下去,此时i往后移一位,即
i++。
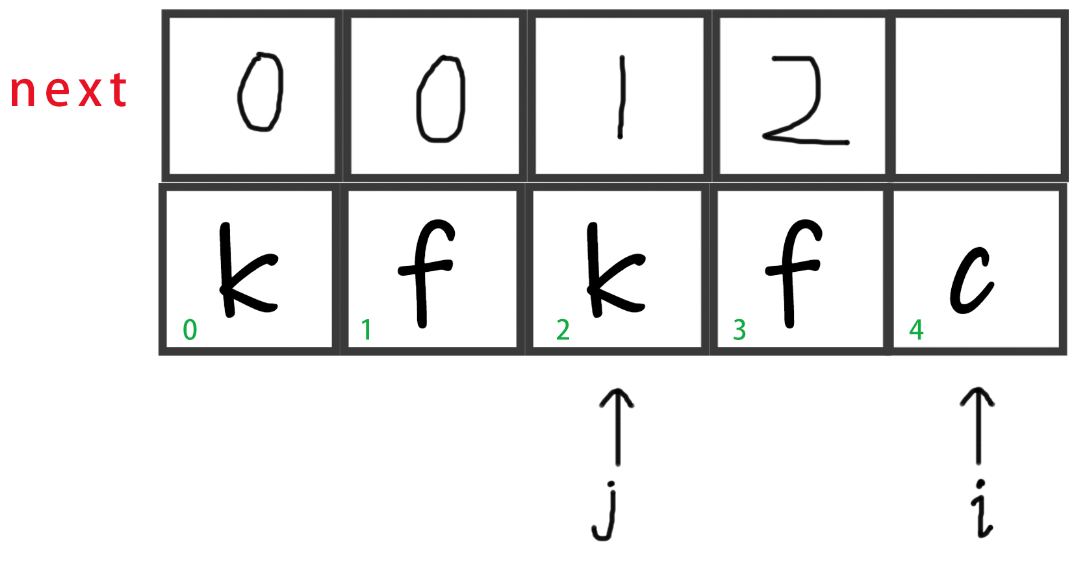
-
此时
str[i] != str[j],而且j不处于首位,所以j回退到next[j - 1]的位置,即退到0。
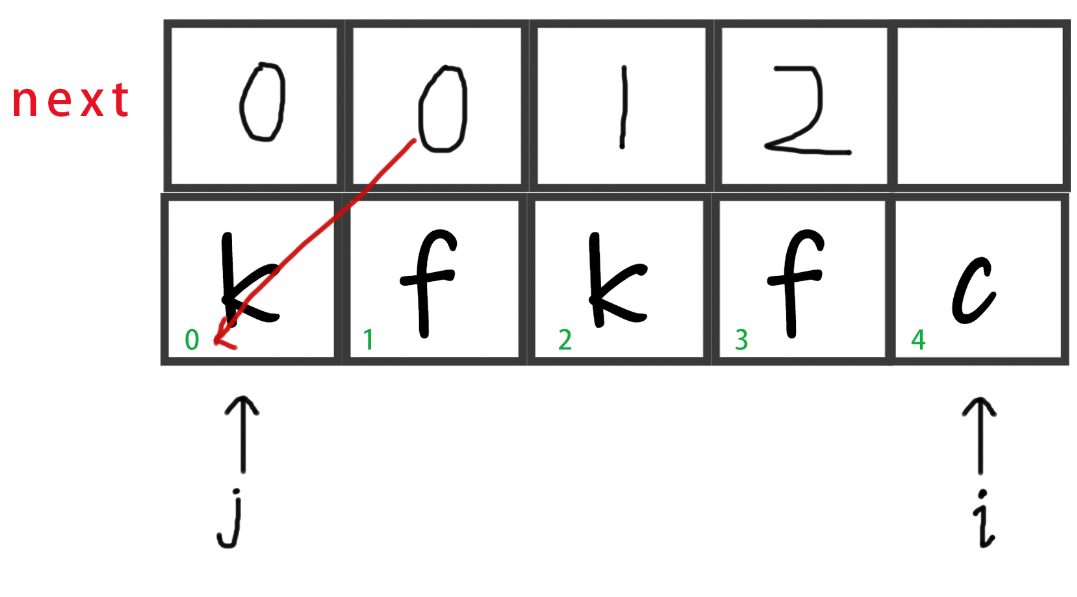
-
接下来给next赋值,此时j=0,所以赋0。
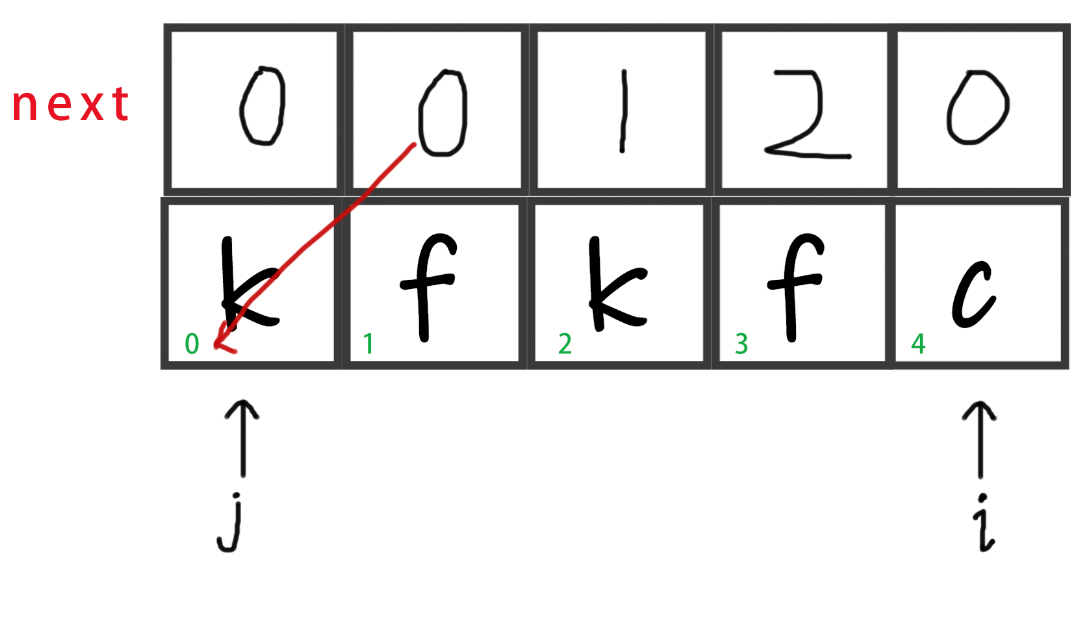
-
i++,到头了,程序结束
时间复杂度分析
O(m+n)
代码
void getNext(const string& str, int* next) {
int j = 0; //j指向后缀
next[0] = j;
for (int i = 1; i < str.size(); i++) { //i从1开始, i指向前缀
while (j > 0 && str[i] != str[j]) { //前后缀不同,此处不可以是if,因为它是连续回退的
j = next[j - 1]; //向前回退
}
if (str[i] == str[j]) //找到了相同的前后缀
j++;
next[i] = j;//将前缀的长度赋给next[i]
}
}
int kmpSearch(string str, string p) {
int next[MAXN]; //next数组
getNext(p, next);//构建next数组
int i = 0, j = 0;
while (i < str.length()) {
if (str[i] == p[j]) { //匹配,指针后移
i++;
j++;
}
else if (j > 0) {//不匹配,根据next回退
j = next[j - 1];
}
else { //第一个就不匹配
i++;
}
if (j == p.size()) //匹配成功
return i - j;
}
return -1; //匹配失败
}
参考资料
Bilibili【喵的算法课】KMP算法【7期】
Bilibili 最浅显易懂的 KMP 算法讲解
Bilibili 帮你把KMP算法学个通透!(求next数组代码篇)
