作业02

第一题

题目

1、根据一个单向链表，复制建立一个双向链表，然后输出双向链表。

思路

由于单向、双向链表的结点不同，所以需要定义两种结点
因为单向、双向链表建立过程的唯一不同就是结点之间的链接方式，所以只需要一个指针指向单向的链表，再按照普通的方式创建双向链表即可。

源程序清单

#include  <iostream>
using namespace  std;
constexpr auto N = 10;  //链表大小
struct  node_one {
    int  data;
    node_one* link;
};

struct node_two {
    int  data;
    node_two* Llink;
    node_two* Rlink;
};

//生成随机的单向链表
node_one* createRandLink()
{
    srand((unsigned int)time(NULL));
    node_one* head = NULL, * p, * q;
    int n = rand() % 20 - 10;   //n为有序链表的起点

    if (N == 0) return NULL;

    head = new node_one;
    p = head;
    p->data = n;
    p->link = NULL;

    for (int i = 1; i < N; i++) {   //生成结点数为N的链表
        q = new node_one;
        q->data = rand() % 40 - 20;  //随机数
        q->link = NULL;
        p->link = q;
        p = q;
    }
    return head;
}

//转换函数
node_two* oneToTwo(node_one* head) {
    node_one* p = head;
    node_two* tp = NULL, *tem = NULL, *thead = NULL;
    if (p != NULL) {
        thead = new node_two;   //开辟第一个结点
        thead->data = p->data;  //对此结点赋值
        thead->Llink = NULL;    //赋左link
        tp = thead; //尾指针指向头
        p = p->link;
    }
    while (p != NULL) {
        tem = new node_two; //新结点
        tem->Llink = tp; tem->Rlink = NULL; tem->data = p->data;    //对新结点赋值
        tp->Rlink = tem; tp = tem;   //连接上新结点，更新双向链表
        p = p->link;    //更新单向链表
    }
    return thead;
}

//作用：逆向输出双向链表
void printTwoLink(node_two* head) {
    node_two* p = head;
    while (p->Rlink != NULL) p = p->Rlink;
    cout << "逆序：\n";
    while (p != NULL) {
        cout << p->data << " <-> ";
        p = p->Llink;
    }
    cout << "\n";
}

//作用：输出单向链表
void printOneLink(node_one* head) {
    node_one* p = head;
    while (p != NULL) {
        cout << p->data << " -> ";
        p = p->link;
    }
    cout << "\n";
}

int main() {
    node_one* ohead = createRandLink();
    printOneLink(ohead);
    node_two* thead = oneToTwo(ohead);
    printTwoLink(thead);
}

运行结果截图

第二题

题目

2、用数组实现栈的基本操作。

思路

由于是数组，所以只需要int一个top来保存栈顶的位置，然后操作就只需对top进行加加减减即可。

源程序清单

char  stack [MAXSIZE];
int top = -1;
int push(char  x){	//if push sucess  return 0,else return 1
	if (top + 1 >= MAXSIZE) return 1;
	top++;
	stack[top] = x;
	return 0;
}
int pop(char& y){	// if pop sucess  return 0,else return 1
	if (top == -1) return 1;
	y = stack[top];
	top--;
	return 0;
}
void disp_stack()   //show the stack
{
	for (int i = top; i >= 0; i--) 
		cout << stack[i] << " ";
	cout << "\n";
}

运行结果截图

（太简不截）

第三题

题目

3、用链表实现栈的基本操作。

   Node  STACK {int  data;  node *link;};
   Node  *top=NULL;

思路

根据栈的特性，我们只看得到顶；而其他元素跟栈顶元素相关（去掉才能看到）。
所以，入栈操作就是在头结点后面加结点，而不是传统意义上的在尾结点后面加。
同理，出栈的话也是对头结点这里的元素进行操作。

源程序清单

#include<iostream>
using namespace std;

struct node {
	int data;
	node* link;
};

class  STACK{ 
public:
	node* top = NULL;
	int push(int a);
	int pop(int& a);
	void printS();
};

//插入操作，a是要插入的元素
int STACK::push(int a) {
	if (top == NULL) {  //没有头就创建
		top = new node;
		top->data = a;  //头结点储存数据（即不带头结点的链表）
		top->link = NULL;
		return 0;
	}
	else {
		node* p = new node;
		p->data = a; p->link = top;	//接到开头
		top = p;    //头结点变成新结点
		return 0;
	}
	return 1;	//插入失败
}

//出栈操作
int STACK::pop(int& a) {
	if (top == NULL) return 1;  //如果已经空了，返回1作为错误标志
	node* p = top;
	top = top->link; a = p->data;
	delete p;   //释放空间
	return 0;
}

//打印栈（从栈顶开始到栈底）
void STACK::printS() {
	node* p = top;
	while (p != NULL) {
		cout << p->data << " ";
		p = p->link;
	}
	cout << "\n";
}

int main() {
	STACK s;
	for (int i = 0; i < 9; i++) {
		if (s.push(i))  //若返回结果为1，说明出问题了
			cout << "入栈失败！\n";
	}
	s.printS();
	int a;
	s.pop(a);
	cout << "pop: " << a << endl;
	s.printS();
	return 0;
}

运行结果截图

（同T2）

第四题

题目

4、实现表达式的计算
设输入的表达式是字母母 a,b,c,……g（字母代表的值自己拟定）
运算符可能是（）± * / % 和 > 遵守一般的次序规则(参照C++中的运算优先级及运算方法)

思路

a,b,c…代表1,2,3
遍历表达式的每一项，如果：
1. 为字母：压入数字栈
2. 为操作符：把这个操作符和栈中的操作符进行优先级比较
  1. 栈为空或者这个操作符优先级高：压入操作符栈
  2. 这个操作符优先级小于栈顶的优先级：把栈顶的操作符和数字栈顶的2个数字进行运算。
3. 为括号：把左括号压入栈后，一切照常。直到碰到右括号后，把左括号到右括号之间的运算符按照（和上一点）相同的规则运算。最后弹出括号。
输出结果

源程序清单

#include<iostream>
#include<cctype>
constexpr int MAXN = 100;
using namespace std;

//获取操作符的优先级
int getPrior(char c) {
    switch (c) {
    case'>':
        return 1;
    case'+':
    case'-':
        return 2;
    case'*':
    case'/':
        return 3;
    case'^':
        return 4;
    case'(':
        return 0;
    }
}

//根据传入的操作符对两个数进行运算，返回运算结果
int getResult(char op, int a, int b) {
    int sum = 1;
    switch (op) {
    case '+':
        return a + b;
    case '-':
        return a - b;
    case '*':
        return a * b;
    case '/':
        if (b == 0) {   //除数为0则退出
            cerr << "除数不能为0！\n";
            exit(1);
        }
        return a / b;
    case '%':
        return a % b;
    case '^':
        for (int i = 0; i < b; i++) sum *= a;
        return sum;
    case '>':
        return a > b;
    default:
        cerr << "存在不符合规则的运算符！\n";
        exit(2);
    }
    return 0;
}

void countSum(char exp[], int& sum) {
    int nstack[MAXN];char ostack[MAXN];
    int ntop = -1, otop = -1;
    int i = 0;  //遍历exp[]

    while (exp[i] != '\0') {
        if (isalpha(tolower(exp[i]))) { //是字母
            // cout << "exp[" << i << "]= " << exp[i] << endl; //测试
            ntop++;
            nstack[ntop] = int(exp[i]) - 'a' + 1;   //转化成数字，压入栈内
        }
        else {       
            switch (exp[i]) {
            case '+':
            case '-':
            case '*':
            case '/':
            case '^':
            case '%':
                if (otop == -1) {   //如果操作符栈为空，直接压入栈
                    otop++;
                    ostack[otop] = exp[i];
                }
                else {
                    if (getPrior(exp[i]) <= getPrior(ostack[otop])) {   //优先级低就计算栈内
                        if (ntop <= 0||otop == -1) {    //表达式有误
                            cerr << "表达式有误！\n";
                            exit(1);
                        }
                        //计算栈内
                        int tem = nstack[ntop];
                        ntop--;
                        nstack[ntop] = getResult(ostack[otop], nstack[ntop], tem);
                        otop--; //操作符出栈
                    }
                    otop++; //入栈
                    ostack[otop] = exp[i]; // 防止不断的推出操作符，最后空栈了;或者ch优先级高了
                }
                break;
            case '(':   //左括号入栈
                otop++;
                ostack[otop] = '(';
                break;
            case')':    //碰到了右括号
                while (ostack[otop] != '(') {
                    if (ntop <= 0 || otop <= 0) {    //表达式有误
                        cerr << "表达式有误！\n";
                        exit(1);
                    }
                    int tem = nstack[ntop];
                    ntop--; //取出操作数
                    nstack[ntop] = getResult(ostack[otop], nstack[ntop], tem);  //计算结果，压入栈
                    otop--; //操作符出栈
                }
                otop--; //把 ( 弹出
                break;
            }
        }
        i++;
    }
    while (otop > -1) {
        if (ntop <= 0) {    //表达式有误
            cerr << "表达式有误！\n";
            exit(1);
        }
        int tem = nstack[ntop--];
        nstack[ntop] = getResult(ostack[otop], nstack[ntop], tem);
        otop--; //操作符出栈
    }
    if (ntop == 0) sum = nstack[ntop];
    else {
        cerr << "wrong！\n";
        exit(1);
    }
}

int main() {
    char exp[MAXN];
    int sum;

    cout << "请输入表达式（26个字母分别对应1~26，请使用小写）:\n";
    cin >> exp;
    
    countSum(exp, sum);
    cout << sum << endl;
}

运行结果截图

第五题

题目

5、实现迷宫问题
要求迷宫大小为m行n列，每个位置可走的方向是上、下、左、右4个方向，迷宫的入口是1，n出口是 m、1。找到路径后在迷宫中用特殊字符表示该路径。

思路

使用DFS算法搜索路径。
由于可以走上下左右四个方向，所以在每一个点位，对这4个方向进行遍历。如果某个方向可以走，就将带有当前坐标和走的方向的序号的信息的struct压入栈。
如果找到了终点，根据栈中的坐标将路径变成*，再输出整个迷宫即可。
如果无路可走，又没有到达终点，就返回上一个格子（出栈），接着遍历剩下的方向（此前保存了走的方向的信息）。
如果最后栈空了，还没有到达终点，就输出找不到路。
注释写得较为详细，思路都在里面了。

源程序清单

#include<iostream>
#include<stack>
constexpr int MAX = 50;	//整个迷宫最大边长
constexpr int DIR = 4;	//方向数
using namespace std;

struct Move {
	int a, b;	//a--行（上下走），b--列（左右走）
};

struct point {	//表示迷宫的点，包括坐标和下一步走的方向
	int x, y, d;//x:行，y:列，d:方向（0~DIR - 1)
	point(int a, int b, int c) {	//构造函数，方便输入
		x = a; y = b; d = c;
	}
	void makePoint(int a, int b, int c) {	//赋值用的函数，方便输入
		x = a; y = b; d = c;
	}
};

class Maze {
public:
	char board[MAX][MAX];	//储存迷宫的样子，由于需要把路变成*，所以类型是char
	int mark[MAX][MAX];	//被走过就是1，没有就是0，其实bool也行；由于不可能出现“一条不通的路和一条通的路都经过这一点”，所以变成1就是1了
	int m = 0, n = 0;	//迷宫的大小，m:行,n:列，人为改变
	Move mv[DIR];	//走的方向——上下左右，DIR是方向的数量，可能不止有上下左右
	stack<point> s;	//用于寻找路的栈，最后要么储存这条路，要么为空表示找不到路。

	Maze(int a, int b);	//构造函数，初始化边界和内部大小，还有移动方向
	void refreshMaze();	//这个函数作用是找到到达终点的路后，把这条路换成*。
	void createMaze();	//创建自定义的迷宫
	void outputMaze();	//输出迷宫（包括边界）
	int getPath(int beg_a, int beg_b, int end_a, int end_b);	//生成路径，前两个参数是起点，后两个是终点。给程序增加更大的灵活性
};


//构造函数，初始化边界和内部大小
Maze::Maze(int a, int b) {
	m = a; n = b;
	for (int i = 0; i < m + 2; i++) {
		for (int j = 0; j < n + 2; j++) {
			board[i][j] = '1';	//把所有的包括边界的格子初始化为1
			mark[i][j] = 0;	//所有的格子都标记为未走过
		}	
	}

	mv[0].a = 0; mv[0].b = -1;	//往左
	mv[1].a = 1; mv[1].b = 0;	//往下
	mv[2].a = -1; mv[2].b = 0;	//往上
	mv[3].a = 0; mv[3].b = 1;	//往右
}

//把路线变成*
void Maze::refreshMaze() {
	while (!s.empty()) {
		int a = s.top().x; 
		int b = s.top().y;
		board[a][b] = '*';
		s.pop();
	}
}

//输入迷宫内部
void Maze::createMaze(){
	cout << "input maze:\n";
	for (int x = 1; x <= m; x++)
		for (int y = 1; y <= n; y++)
			cin >> board[x][y];
}

//输出迷宫
void Maze::outputMaze() {
	cout << "output maze:\n";
	for (int i = 0; i <= m + 1; i++) {
		for (int j = 0; j <= n + 1; j++) {
			cout << board[i][j] << " ";
		}
		cout << "\n";	
	}
	cout << "\n";
}

//得到路径,beg_a:起点行数（纵坐标），beg_b:起点列数（横坐标）
int Maze::getPath(int beg_a, int beg_b, int end_a, int end_b) {
	beg_a = 1; beg_b = n;	//起点：右上，终点：左下
	end_a = m; end_b = 1;	//由于题目的起点和终点都已经确定，所以就在这里写死了，无论传进来什么都会变的

	if (board[1][n] == '1' || board[m][1] == '1') return 1;	//如果起点终点有到不了的，直接返回
	point tem_p(beg_a, beg_b, -1);	//初始化
	s.push(tem_p);		//先将起点压入栈
	mark[beg_a][beg_b] = 1;	//起点走过了

	int nowRow, nowCol;	//现在的行和列
	int nextRow, nextCol; //下一个方向的行和列
	int dir;	//方向数

	tem_p.makePoint(0, 0, -1); s.push(tem_p);	//先加一个点进去，交给下面的while循环判断（为了凑成while）

	//此处使用DFS
	while (1) { //栈不空
		s.pop();	//如果这个点后面的路行不通，就退回去一格，看看有没有其他方向
		if (s.empty()) return 1;//如果栈空了，直接结束
		nowRow = s.top().x;
		nowCol = s.top().y;	//更新如今的坐标为：回退一格后的坐标
		dir = s.top().d;	//接着上次的方向继续遍历下去

		while (dir < DIR - 1) {	//遍历每一个方向，由于dir是从-1开始（下面是++dir，先加再赋值的），所以DIR要-1
			nextRow = nowRow + mv[++dir].a;
			nextCol = nowCol + mv[dir].b;	//下一步走到的坐标
			if (nextRow == end_a && nextCol == end_b) {	//找到了终点
				if (s.top().x == 0 && s.top().y == 0) s.pop();	//保险起见，免得多塞了一个点进去
				tem_p.makePoint(nowRow, nowCol, dir); s.push(tem_p);
				tem_p.makePoint(nextRow, nextCol, dir); s.push(tem_p);	//把终点也推进去
				refreshMaze();	//把路变成*
				outputMaze();	//输出最后的迷宫
				return 0;	//记得直接结束
			}
			if (board[nextRow][nextCol] == '0' && mark[nextRow][nextCol] == 0) {	//这个位置可以走，而且没走过
				mark[nextRow][nextCol] = 1;	//这个点要走了

				s.top().x = nowRow;
				s.top().y = nowCol;	//坐标的更新有一种“滞后性”，这样相当于提前找下下个点
				s.top().d = dir;	//更新当前点位的方向
				
				tem_p.makePoint(0, 0, -1);	s.push(tem_p);//这就是滞后性
				nowRow = nextRow; nowCol = nextCol;	//把当前坐标更新为下一个坐标
				dir = -1;	//把方向也更新一下
			}
		}
	}
	return 1;
}

int main() {
	int m, n;
	cout << "input m n:\n";
	cin >> m >> n;

	Maze mz(m, n);
	mz.createMaze();
	mz.outputMaze();
	if (mz.getPath(1, n, m, 1)) {	//因为返回值为1的话，就表示不能生成（人为定义的）
		cout << "Error! No path!\n";
	}
	return 0;
}

kokoro的小站

数据结构作业——栈

作业02

第一题

题目

思路

源程序清单

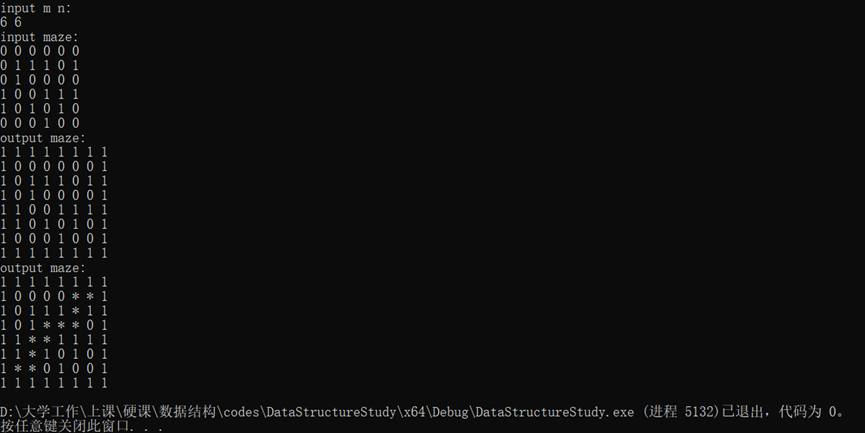
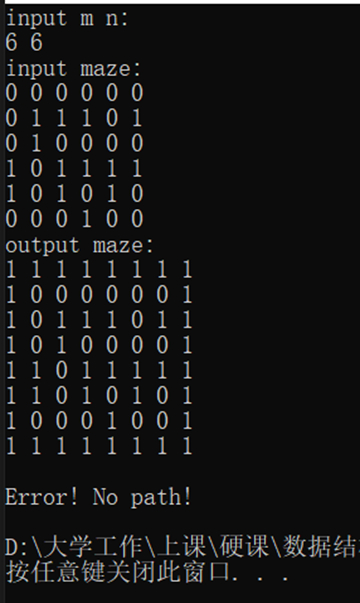
运行结果截图

第二题

题目

思路

源程序清单

运行结果截图

第三题

题目

思路

源程序清单

运行结果截图

第四题

题目

思路

源程序清单

运行结果截图

第五题

题目

思路

源程序清单

运行结果截图

wangkewei172

作业02

第一题

题目

思路

源程序清单

运行结果截图

第二题

题目

思路

源程序清单

运行结果截图

第三题

题目

思路

源程序清单

运行结果截图

第四题

题目

思路

源程序清单

运行结果截图

第五题

题目

思路

源程序清单

运行结果截图

数据结构作业——排序

利用Python批量修改多个ass字幕文件

wangkewei172