作业04 树

第一题

题目

假设二叉树T是按标准形式存贮的，试编写一个把该树中每个结点的左右子结点进行对换的C++函数。

思路

此处的“标准形式”为数据+指向子结点的指针
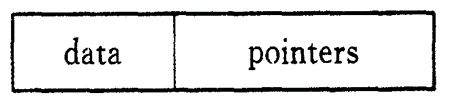
利用递归，对根结点下面的两个子结点进行交换。返回条件是根结点为空。

源程序清单

//node的结构
struct node {
	int data;
	node* leftChild;	//左子结点
	node* rightChild;	//右子结点
};


//交换结点
//从上到下的顺序换
void swapBinaryTree(node* &head) {
	if (head == NULL) return;   //basecase
	swap(head->leftChild, head->rightChild);	//先换上面的，把它移到最下面也可以
	swapBinaryTree(head->leftChild);
	swapBinaryTree(head->rightChild);
}

第二题

题目

编写一个利用栈来实现后序遍历一棵给定的二叉树的c++函数

思路

题目说利用栈，也就是说可以利用递归。
后序遍历的顺序：左右根
遍历整棵树等于遍历根结点的左、右子树，就这样一直分到最小

源程序清单

//node的结构
struct node {
	int data;
	node* leftChild;	//左子结点
	node* rightChild;	//右子结点
};

//利用栈（即递归）实现后序遍历
void printBinaryTree(node* head) {
	if (head == NULL) {	//某结点为空，返回
		return;
	}

	//左后中的顺序输出
	printBinaryTree(head->leftChild);	
	printBinaryTree(head->rightChild);
	cout << head->data << " ";
}

第三题

题目

如果T是一棵有序树，T’是与T相对应的二叉树。假定T’已按标准形式被存贮，试为下面各小题分别编写一个C++函数：
（1）按前序输出树T的结点值。
（2）按后序输出树T的结点值。
（3）输出树T的叶子结点值。
（4）求出树T的次数。

思路

前面两问就是前、后序遍历并输出，与第二题思路基本一致。
第三问涉及到树转化为二叉树后，叶子结点的变化。下面是一颗树及其对应的二叉树：

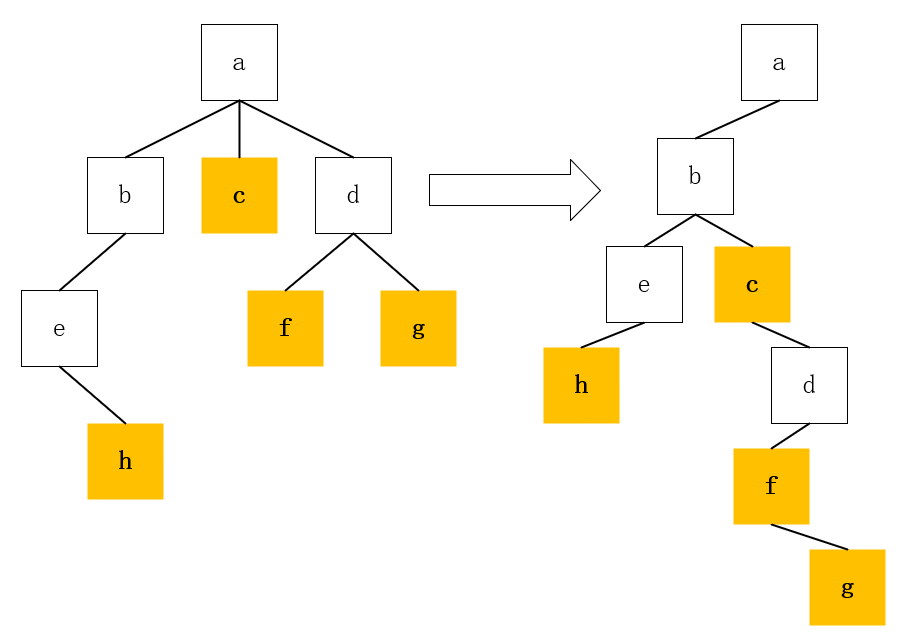
因为在转化过程中，

树的非左子结点变成了它左子结点及其右子结点（h从e的右子结点变成了e的左子结点）
兄弟结点转化为了它的右子结点（c、d从a的右子结点变成了b的右子结点）。
而左子结点照旧。
总之，只要它有子结点，一定是先变成它的左子结点，再变成其他的。
所以，如果二叉树的一个结点没有左子结点，说明它既没有右子结点，又没有左子结点，即它是叶子结点。
于是，我们只需要看二叉树的一个结点是不是没有左子结点，没有就说明它是树的叶子结点。

第四问求次数。已知一个树的次数等于它最多的某个结点的子结点数，由于树变成二叉树时，兄弟结点变成了它的连续右子结点。所以我们看二叉树的最大的连续右子结点的数量就可以求出次数了。

源程序清单


//计算当前结点的最大右连续子结点
// 从自己开始算起，所以head也算数，所以sum初始值为1
int countConRight(node* head) {
	int sum = 1;
	if (head->rightChild != NULL)	// 有右子结点就计数并往右走
		sum += countConRight(head->rightChild);
	else	// 没有右子结点了，作为最大值返回
		return sum;

}

//计算树的次数
//树的次数就是二叉树的左孩子的连续右孩子（包括自己）的最大值
int countTimes(node* head) {
	if (head == NULL) return 0;
	
	int num = countConRight(head);

	//应该还有更优的方法
	//取当前结点的最大右连续数和左右子树的进行比较，取最大值
	//由于根结点不可能有右子结点，所以不用对特殊情况进行处理。
	num = max(max(countTimes(head->rightChild),countTimes(head->leftChild)),num);
	return num;
}

第四题

题目

假设二叉树T的结点值是字符，已知树T中结点的前序和中序，试编写一个把树T按标准形式进行存贮的C++函数。

思路

首先，如果结点的值重复，会有多种情况，所以我们这里假设值不重复。
前序的特点是：从左到右都是根结点；
中序的特点是：某个结点的左右结点一定都在它的两边。
于是我们的思路就出来了：遍历前序，找到它在中序里面的位置，它左边就是左子树，右边就是右子树，这样就可以把中序不断分层成子树。
比如，前序的第一个值为根结点，去中序中找到这个结点，它的左边就是根结点的左子树，右边就是根结点的右子树。接着在它的左边找到前序的第二个值的位置，又把它分成左右子树…（以下给出部分过程）
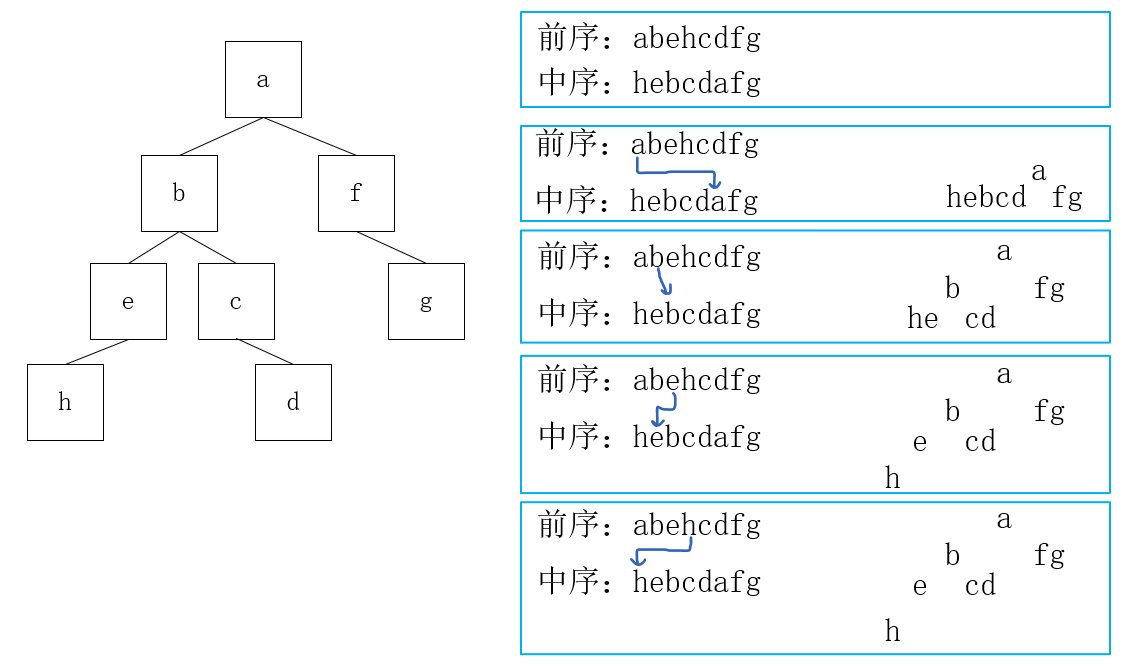
我们需要一个指针指向前序，在每次递归中都向后移一步；然后每次递归都把对应的左右子树当作“整棵树”传下去。

源程序清单

本程序参考了这篇博客

//t7，利用二叉树的前序和中序建立树
//由于如果有重复数值可能会有多种情况，所以我们这里假设没有重复数值
//前序的第一个为根节点，中序的根节点左右方分别是左右子树，所以可以利用这一点递归
node* makeTreeByPreIno(char pre[], char ino[], int n) {	//传入的两个参数分别为：前序、中序、数组长度
	if (n == 0) {	//当数组长度为0时，返回NULL
		return NULL;
	}

	// 1.首先取前序的首个作为根节点的值
	node* head = new node;
	head->data = pre[0];

	// 2.接着在中序里面找到这个值
	char* p = ino;	//作为寻找该值的指针
	for (; p < ino + n; p++) {
		if (*p == pre[0])	//找到根节点的位置（值不重复）
			break;
	}

	int leftNum = p - ino;	//左子树的大小，等于中序里面找到的根节点的位置减去开头的位置

	// 3.找到后，它（中序）的左边为左子树，右边为右子树，开始递归

	// 首先是左子树，pre[0]已经是根节点了，所以需要“后移”一位
	// 中序的“子树范围”受leftNum（左子树大小）限制，所以相当于ino和leftNum一起“截取”了该子树
	head->leftChild = makeTreeByPreIno(pre + 1, ino, leftNum);	

	// 接着是右子树，它的起始位置等于起点加左子树的大小。
	// 右子树的起点则为p+1，长度为总长减去左子树长（找到的根节点后面的部分）
	// 而长度则为剩下一部分的长度（传入的长度减一，因为前序的第一个已经是根节点了，所以总长度减一）减去左子树长度
	head->rightChild = makeTreeByPreIno(pre + 1 + leftNum, p + 1, n - leftNum - 1);	

	return head;
}

第五题

题目

在二叉树T中，如果非叶子结点都有两棵非空子树，那么称二叉树T是一棵完全二叉树。试编写一个判断给定的二叉树是否为完全二叉树的C++函数。

思路

题目说了，非叶子结点都有两棵非空子树，这就是个非常好的递归basecase。
只有左右子树均为完全二叉树才算是完全二叉树。而当某个结点左右子结点都为空时，我们就认为它是完全二叉树（只有一个结点的完全二叉树）。

源程序清单

//判断是不是完全二叉树
bool isCompleteBT(node* head) {
	if (head->leftChild == NULL && 
		head->rightChild == NULL) {	//左右子树均为空，说明是叶子结点，返回真
		return true;
	}
	else if (head->leftChild != NULL && head->rightChild != NULL) {	//如果左右子树均不为空，递归下去
		return isCompleteBT(head->leftChild) && isCompleteBT(head->rightChild);	
	}
	else
		return false;	//一个为空，一个不为空，不是完全二叉树
}

第六题

题目

现给出两棵二叉树相似的定义如下：如果这两棵二叉树皆为空；或者这两棵二叉树的根结点的左子树和右子树是分别相似的，那么我们称这两棵二叉树是相似的。试编写一个判断两棵给定的二叉树是否相似的C++函数。

白话：判断两棵二叉树是不是结构一样。

思路

根据题目，很明显可以使用递归。两树均为空、左右子树相似为相似，其他不相似。
本题和上一题基本思路一致，区别只在于判断条件的更改。

源程序清单

//判断两树是否相似
bool isSimilarTree(node* tree1, node* tree2) {
	if (tree1 == NULL && tree2 == NULL)	//两棵子树为空，说明相似
		return true;
	else if (tree1 != NULL && tree2 != NULL)	//没有为空的子树就接着判断子树的相似；
		return isSimilarTree(tree1->leftChild, tree2->leftChild)
		&& isSimilarTree(tree1->rightChild, tree2->rightChild);	//左右子树是否分别相似
	else	//如果一个为空一个不为空，就说明不相似
		return false;
}

第七题

题目

设二叉树T已按前序附带一个标志位和一个右指针的顺序存贮方法存放，试编写一个把树T转换成由标准形式进行存贮的树T’的C++函数。

思路

首先，这种储存方式是：
- 标志位 (ltag)：为0表示它下一个是它的左子树；为1表示它后面没有子结点
- 右指针 (rchild)：保存该结点的右子结点的位置，如果不存在右结点就为-1。
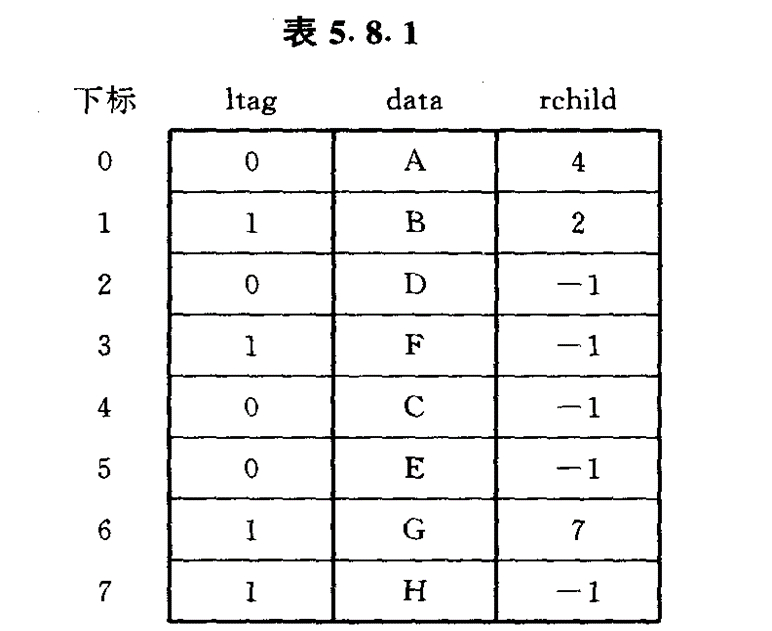
我们可以正常使用递归，建立左右子树，根据标志位和右指针的值“跳”到相应的地方接着建立。
以上图为例。从A开始，ltag=0说明B是A的左子结点；rchild=4说明C是A的右子结点。于是A的左指针指向B，右指针指向C，接着对B、C进行同样的操作。

源程序清单

//以前序形式存放结点附加左标志位和右指针，以结构体数组的形式储存树
struct node {
	char data;	// 结点的值
	int ltag;	// 如果它等于0，说明它后面是左子树。如果等于1，则表示它没有左子结点
	int rchild;	// 右子结点的位置，如果它为-1，则说明它没有右节点
};

// 标准形式储存的二叉树
struct bnode {
public:
	char data;	//值
	bnode* lbnode;	//左结点
	bnode* rbnode;	//右结点
};

//附加左标志位和右指针 转化为 标准形式储存，pos是位置，tree是结点数组
bnode* convertPreToBin(int pos,node tree[]) {
	bnode* bhead = new bnode;
	bhead->data = tree[pos].data;	//对该结点赋值

	if (tree[pos].ltag && tree[pos].rchild == -1) {	//左右都为空
		bhead->lbnode = NULL;
		bhead->rbnode = NULL;
		return bhead;	//说明本分支到头了，就返回
	}
	if (!tree[pos].ltag) {	// 左子结点存在
		bhead->lbnode = convertPreToBin(pos + 1, tree);	//后面一个就是左子结点
	}
	if (tree[pos].rchild != -1) {	//右子结点存在
		bhead->rbnode = convertPreToBin(tree[pos].rchild, tree);	//跳到右子结点的位置
	}
	return bhead;
}

第八题

题目

假设二叉树T已按前序附加两个标志位的顺序存贮方法存放，且a是T中一个结点的值，试编写一个寻找结点a的父结点的C++函数。

思路

首先，附带两个标志位的结构为：
1. 左标志位：
  - 0: 该结点后面的结点是它的左子树
  - 1: 该结点无左子结点
2. 右标志位：
  - 0: 有右子树
  - 1: 无右子树
遍历方式：设立一个栈，遇到有右子树的就入栈，遇到无左子结点的就出栈。这样该结点就和它的右子结点匹配上了。
既然如此，我们要寻找父节点，就可以在遍历的途中寻找。一个结点要么是某个结点的左子结点，要么是某个结点的右子结点，根据两个标志位，我们可以很清楚地知道上一个结点的子结点情况。
于是，假设我们遍历到了a，那么我们就去看它前一个（因为是数组）的左标志位。
如果左标志位为0，说明a是前一个的左子结点，返回这个结点的位置。
如果左标志位为1，说明a是某个结点的右子结点，于是返回栈顶元素，即该结点的地址。

源程序清单

# include <stack>
struct lrnode {
	char data;
	char ltag, rtag;	//值为0说明有对应的结点，为1说明没有
};

// 找到父节点，返回父节点的地址。
// 可以通过栈来模拟向二叉树的转化，从而得出父节点
lrnode* findFatherNode(lrnode tree[], char a, int length) {	//传入的变量为：附加2个标志位储存的树，结点a的值，树的结点数（数组长度）
	stack<lrnode*> treeStk;
	if (tree == NULL || tree[0].data == a) {
		cerr << "找不到父节点！\n";
		return NULL;	//如果树不存在或者没有父节点，返回空；
	}

	int i = 0;
	for (; i < length; i++) {	///模拟建树
		if (tree[i].data == a) break;	//找到了
		if (tree[i].rtag == '0') 
			treeStk.push(&tree[i]);	//如果它存在右子结点，就入栈

		if (tree[i].ltag == '1')	//如果这个结点没有左子结点，说明下一个结点就是某个结点的右子结点
			treeStk.pop();
	}

	if (i == length || i == 0) {	//没有找到值为a的结点，或者为根结点
		cerr << "没有找到值为a的结点或为根结点！\n";
		return NULL;
	}
	else {	//这个结点存在，就去找它的父节点
		if (tree[i - 1].ltag == '0') //说明这个结点是上个结点的子结点
			return &tree[i - 1];
		else if (!treeStk.empty())	//如果栈不空（数组可能有错）
			return treeStk.top();	//如果上一个结点没有左子结点，说明这个结点的父节点在栈中
		else
			return NULL;
	}
}

第九题

题目

假设二叉树T是一棵穿线树，试编写一个按前序遍历树T的C++函数。（不允许用递归程序，也不使用数组，只允许增加个别变量）

ps:此处说的穿线树是指线索二叉树，在本题中指按中序顺序的线索二叉树。

思路

首先知道线索二叉树是什么：
- 我们知道，二叉树总会有n + 1个空指针。因为一个结点2个指针，一共n个结点，有n - 1个指针指向了子结点（根结点不需要被指，画个图就可以看出来了）
- 于是我们建立了线索二叉树去利用这些空指针。
- 线索二叉树分为前序、中序、后序，以中序为例，我们首先列出一颗标准二叉树的中序遍历顺序：
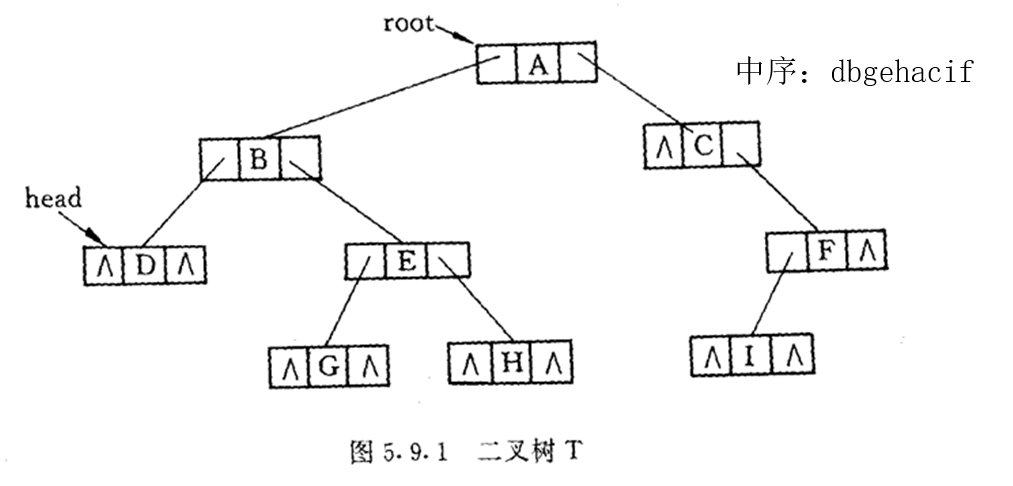
- 对每个结点，我们看它缺了哪边的“腿”（即指针为空），然后把它指向对应顺序的对应边。
  举例说明，C缺了左腿，因为是中序，我们便看中序里面C的左边是什么——是A，于是C的左指针就指向A。
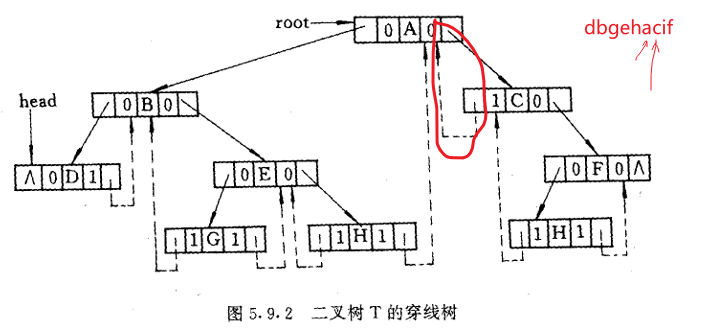
- 对于处于首尾的元素，由于两边没有可以指的结点，于是我们令他指向空NULL。
通过线索二叉树的特性我们可以知道，左子结点的空右指针一定会指向父结点。
由于我们是要对它前序输出，所以我们可以建立一个循环：
1. 开局就一直往左“跑”到底，边跑边输出。
2. 然后通过左子结点的特性回溯（不停往右跑），一直回溯到存在右子结点的结点。
3. 接着到这个结点的右子结点，重复步骤1

源程序清单

struct node {	//穿线树的结构
	char data;	//值
	int ltag = 0, rtag = 0; //当ltag = 0时，lchild指向它的左子结点；当ltag = 1时，lchild指向它对应顺序（比如中序）的前一个值的结点
	node* lchild, * rchild;	
};

//将中序穿线树以前序方式输出
void prePrint(node* head) {
	while(head != NULL){	//如果到了最后一个结点（因为不管哪种遍历顺序，最后一个元素都是相同的），它指向的是空。
		cout << head->data << " ";	//因为是前序，所以先输出
		if (head->ltag == 0 && head->lchild) {	//一直往左跑，跑到底。（如果左子结点存在且不为空，这里省略了!=NULL）
			head = head->lchild;
			continue;
		}

		if (head->ltag == 1 || head->lchild == NULL) {
			while (head->rchild != NULL && head->rtag != 0)	//往“回”跑，跑到有右结点的地方。（如果右子结点存在且不为空）
				head = head->rchild;
			head = head->rchild;	//接着到这个右结点这里
		}
	}
}

kokoro的小站

数据结构作业——树

作业04 树

第一题

题目

思路

源程序清单

第二题

题目

思路

源程序清单

第三题

题目

思路

源程序清单

第四题

题目

思路

源程序清单

第五题

题目

思路

源程序清单

第六题

题目

思路

源程序清单

第七题

题目

思路

源程序清单

第八题

题目

思路

源程序清单

第九题

题目

思路

源程序清单

wangkewei172

作业04 树

第一题

题目

思路

源程序清单

第二题

题目

思路

源程序清单

第三题

题目

思路

源程序清单

第四题

题目

思路

源程序清单

第五题

题目

思路

源程序清单

第六题

题目

思路

源程序清单

第七题

题目

思路

源程序清单

第八题

题目

思路

源程序清单

第九题

题目

思路

源程序清单

数据结构学习笔记——排序

python实现朋友圈自动点赞（前台）

wangkewei172